题目内容
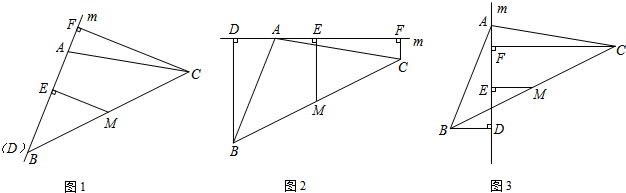
 小强和小明去测量一座古塔的高度,他们在离古塔60米的A处,用测角仪器测得塔顶的仰角为30°,若测角仪器高AD=1.5米,则古塔BE的高为
小强和小明去测量一座古塔的高度,他们在离古塔60米的A处,用测角仪器测得塔顶的仰角为30°,若测角仪器高AD=1.5米,则古塔BE的高为考点:解直角三角形的应用-仰角俯角问题
专题:
分析:过A作AF⊥BE于点F,可得四边形ADEF为矩形,可得EF=AD=1.5m,AF=DE=60m,在Rt△ABF中,∠BAF=30°,利用三角函数求出BF的长度,继而可求得BE的高度.
解答:解:过A作AF⊥BE于点F,
∴四边形ADEF为矩形,
∴EF=AD=1.5m,AF=DE=60m,
在Rt△ABF中,
∵∠BAF=30°,
∴tan∠BAF=
,
∴BF=AF•tan30°=60×
=20
(m),
∴BE=20
+1.5(m).
故答案为:20
+1.5.
∴四边形ADEF为矩形,

∴EF=AD=1.5m,AF=DE=60m,
在Rt△ABF中,
∵∠BAF=30°,
∴tan∠BAF=
| BF |
| AF |
∴BF=AF•tan30°=60×
| ||
| 3 |
| 3 |
∴BE=20
| 3 |
故答案为:20
| 3 |
点评:本题考查了解直角三角形的应用,解答本题关键是根据仰角构造直角三角形,利用三角函数的知识表示出相关线段的长度.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目