题目内容
17.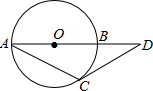 如图,已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上一点,DC是⊙O的切线,C是切点,连结AC.若∠CAB=30°,则BD的长为( )
如图,已知⊙O的半径为R,AB是⊙O的直径,D是AB延长线上一点,DC是⊙O的切线,C是切点,连结AC.若∠CAB=30°,则BD的长为( )| A. | R | B. | $\sqrt{3}$R | C. | 2R | D. | $\frac{\sqrt{3}}{2}$R |
分析 连接OC,由DC是⊙O的切线,则△DCO是直角三角形;由圆周角定理可得∠DOC=2∠CAB=60°,则OD=2OC=20B,BD的长即可求出.
解答  解:连接OC.
解:连接OC.
∵DC是⊙O的切线,
∴OC⊥CD,即∠OCD=90°.
又∵∠BOC=2∠A=60°,
∴Rt△DOC中,∠D=30°,
∴OD=2OC=20B=OB+BD,
∴BD=OB=R.
故选A.
点评 本题考查了切线的性质及圆周角定理.解答该题的切入点是从切线的性质入手,推知△DOC为含30度角的直角三角形.

练习册系列答案
相关题目
8. 如图,在⊙O中,∠ACB=32°,则∠AOB的度数是( )
如图,在⊙O中,∠ACB=32°,则∠AOB的度数是( )
 如图,在⊙O中,∠ACB=32°,则∠AOB的度数是( )
如图,在⊙O中,∠ACB=32°,则∠AOB的度数是( )| A. | 16° | B. | 32° | C. | 64° | D. | 74° |
12.下列运算正确的是( )
| A. | a-2a=a | B. | (-a2)3=-a6 | C. | a6÷a3=a2 | D. | a3-a2=a |
2.两圆的半径为5cm和3cm,若圆心距为7cm,则两圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
 如图,?ABCD的对角线相交于O,且AB=6,△OCD的周长为23,?ABCD的两条对角线的和是34.
如图,?ABCD的对角线相交于O,且AB=6,△OCD的周长为23,?ABCD的两条对角线的和是34.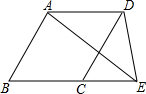 如图,?ABCD中,E是BC延长线上一点,连接AE,DE,若?ABCD的面积为24,则△ADE的面积为12.
如图,?ABCD中,E是BC延长线上一点,连接AE,DE,若?ABCD的面积为24,则△ADE的面积为12.