题目内容
3.求方程2x2+xy-y2=14的整数解.分析 首先把2x2+xy-y2=14左边分解为(2x-y)(x+y)=14,进一步把14分解成两个整数的乘积,进一步建立方程组得出答案即可.
解答 解:∵2x2+xy-y2=(2x-y)(x+y),14=1×14=(-1)×(-14)=2×7=(-2)×(-7),
∴$\left\{\begin{array}{l}{2x-y=1}\\{x+y=14}\end{array}\right.$,$\left\{\begin{array}{l}{2x-y=14}\\{x+y=1}\end{array}\right.$,$\left\{\begin{array}{l}{2x-y=-1}\\{x+y=-14}\end{array}\right.$,$\left\{\begin{array}{l}{2x-y=-14}\\{x+y=-1}\end{array}\right.$,$\left\{\begin{array}{l}{2x-y=2}\\{x+y=7}\end{array}\right.$,$\left\{\begin{array}{l}{2x-y=7}\\{x+y=2}\end{array}\right.$,$\left\{\begin{array}{l}{2x-y=-2}\\{x+y=-7}\end{array}\right.$,$\left\{\begin{array}{l}{2x-y=-7}\\{x+y=-2}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=5}\\{y=9}\end{array}\right.$,$\left\{\begin{array}{l}{x=5}\\{y=-4}\end{array}\right.$,$\left\{\begin{array}{l}{x=-5}\\{y=4}\end{array}\right.$,$\left\{\begin{array}{l}{x=-5}\\{y=4}\end{array}\right.$,$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$,$\left\{\begin{array}{l}{x=-3}\\{y=-4}\end{array}\right.$,$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$.
点评 此题考查因式分解与二元一次方程组的实际运用,掌握因式分解的方法,注意分类讨论思想的运用.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案| 运往地 车型 | 甲 地(元/辆) | 乙 地(元/辆) |
| 大货车 | 700 | 600 |
| 小货车 | 500 | 450 |
(2)如果各安排9辆货车前往甲、乙两地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为W元,求出W与a的函数关系式.(写出自变量取值范围)
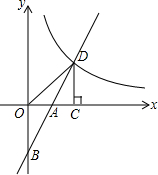 如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A.B两点,与双曲线y=$\frac{k}{x}$(x>0)交于点D,过点D作DC⊥x轴,垂足为C,且点A是OC的中点,连接OD,
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A.B两点,与双曲线y=$\frac{k}{x}$(x>0)交于点D,过点D作DC⊥x轴,垂足为C,且点A是OC的中点,连接OD,
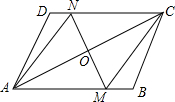 如图,在?ABCD中,点O是对角线AC的中点,过点O的直线MN分别交AB、CD于点M、N,连结AN,CM.
如图,在?ABCD中,点O是对角线AC的中点,过点O的直线MN分别交AB、CD于点M、N,连结AN,CM.