题目内容

在△ABC和△A1B1C1中，∠A=∠A1，
AB
A1B1
=
AC
A1C1
，可得出△ABC
 
△A1B1C1，理由是
 
．
考点：相似三角形的判定
专题：常规题型
分析：根据两组对应边的比相等且夹角对应相等的两个三角形相似进行判定．
解答：解：当∠A=∠A1，
AB
A1B1
=
AC
A1C1
，可得出△ABC∽△A1B1C1，理由是两组对应边的比相等且夹角对应相等的两个三角形相似．
故答案为：∽，两组对应边的比相等且夹角对应相等的两个三角形相似．
点评：本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似．
练习册系列答案
相关题目
若
a-3
+（b-4）2+|c+5|=0，求2a-3b+4c的值．
若
1
5
x3y2k+1与-
7
3
x3y8是同类项，则k=（　　）
A、3.5B、4
C、8D、以上都不对
从0～9这些自然数中，任取一个，是4的倍数的概率是
 
．
我国深潜器目前最大的深潜极限为7062.68m，某天深潜器在海面下1800米处作业（如图），测得正前方海底沉船C的俯角为45°，该深潜器在同一深度向正前方直线航行2000米到B点，此时测得海底沉船C的俯角为60°．
（1）沉船C是否在深潜极限范围内？并说明理由；
（2）现要打捞沉船，打涝时沉船竖直上升，上升速度为200米/时，求该沉船从开始上升直至回到海面的时间．（精确到0.1h）（参考数据：
2
≈1.414，
3
≈1.732）
如图，⊙O是以原点为圆心，
2
为半径的圆，点P是直线y=-x+4上的一点，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（　　）
A、2
B、4
C、3
2
-1
D、
6
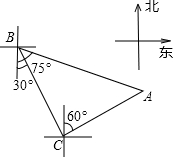轮船从B处以每小时40海里的速度沿南偏东30°方向匀速航行，轮船航行1.5小时到达C处，在C处观测灯塔A位于北偏东60°方向上，且与C处相距80海里，则B处与灯塔A的距离是
 
海里．
解方程
①2（2x-3）=6x-5    
②
2x+6
5
-1=
10-2x
6
    
③
x+11
3
-
2-x
4
=2．
如图，点O在△ABC内，且到三边的距离相等，若∠A=60°，则∠BOC=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网