题目内容
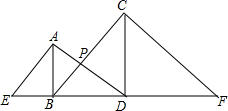如图，运河边上移栽了两棵老树AB、CD，它们相距20m，分别自两树上高出地面3m、4m的A、C处，向两侧地面上的点E和D、B和F处用绳索拉紧，以固定老树，那么绳索AD与BC的交点P离地面的高度为多少米？考点：相似三角形的应用
专题：
分析：过点P作PH⊥BD于H，根据△ABP和△DCP相似求出
，再求出
，然后利用△ABD和△PHD相似列式计算即可得解．
| DP |
| AP |
| DP |
| AD |
解答：
解：如图，过点P作PH⊥BD于H，
∵大树AB、CD都与地面垂直，
∴△ABP∽△DCP，
∴
=
=
，
∴
=
=
，
∵PH、AB都垂直于BD，
∴△ABD∽△PHD，
∴
=
，
即
=
，
∴PH=
，
答：绳索AD与BC的交点P离地面的高度为
米．
解：如图，过点P作PH⊥BD于H，∵大树AB、CD都与地面垂直，
∴△ABP∽△DCP，
∴
| DP |
| AP |
| CD |
| AB |
| 4 |
| 3 |
∴
| DP |
| AD |
| 4 |
| 3+4 |
| 4 |
| 7 |
∵PH、AB都垂直于BD，
∴△ABD∽△PHD，
∴
| PH |
| AB |
| DP |
| AD |
即
| PH |
| 3 |
| 4 |
| 7 |
∴PH=
| 12 |
| 7 |
答：绳索AD与BC的交点P离地面的高度为
| 12 |
| 7 |
点评：本题考查了相似三角形的应用，主要利用了相似三角形对应边成比例的性质，熟记性质是解题的关键．
练习册系列答案
相关题目
如图，已知l1∥l2，α=3m-1°，且20°＜m＜40°，求β的取值范围．
如图，等腰△ABC的底边BC=10cm，顶角为120°，求它的外接圆的直径．