题目内容
已知x=
,y=
,求代数式
+
的值.
| 1 | ||
2+
|
| 1 | ||
2-
|
| 1 |
| x+1 |
| 1 |
| y+1 |
考点:二次根式的化简求值
专题:计算题
分析:先分母有理化得到x=2-
,y=2+
,则可计算出x+y=4,xy=1,再把原式通分得到原式=
,然后利用整体代入的方法计算.
| 3 |
| 3 |
| x+y+2 |
| xy+(x+y)+1 |
解答:解:∵x=
,y=
,
∴x=2-
,y=2+
,
∴x+y=4,xy=1,
∴原式=
=
=
=1.
| 1 | ||
2+
|
| 1 | ||
2-
|
∴x=2-
| 3 |
| 3 |
∴x+y=4,xy=1,
∴原式=
| x+1+y+1 |
| (x+1)(y+1) |
=
| x+y+2 |
| xy+(x+y)+1 |
=
| 4+2 |
| 1+4+1 |
=1.
点评:本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
相关题目
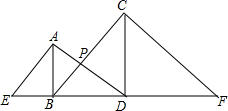 如图,运河边上移栽了两棵老树AB、CD,它们相距20m,分别自两树上高出地面3m、4m的A、C处,向两侧地面上的点E和D、B和F处用绳索拉紧,以固定老树,那么绳索AD与BC的交点P离地面的高度为多少米?
如图,运河边上移栽了两棵老树AB、CD,它们相距20m,分别自两树上高出地面3m、4m的A、C处,向两侧地面上的点E和D、B和F处用绳索拉紧,以固定老树,那么绳索AD与BC的交点P离地面的高度为多少米?