题目内容
 如图,已知l1∥l2,α=3m-1°,且20°<m<40°,求β的取值范围.
如图,已知l1∥l2,α=3m-1°,且20°<m<40°,求β的取值范围.考点:平行线的性质,解一元一次不等式组
专题:计算题
分析:先根据平行线的性质得α+β=180°,则β=181°-3m,再用β表示m得到m=
(181°-β),则20°<
(181°-β)<40°,然后解关于β的不等式组即可.
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:∵l1∥l2,
∴α+β=180°,
而α=3m-1°,
∴β=180°-3m+1,
∴m=
(181°-β),
∵20°<m<40°,
∴20°<
(181°-β)<40°,
解得61°<β<121°,
即β的取值范围为61°<β<121°.
∴α+β=180°,
而α=3m-1°,
∴β=180°-3m+1,
∴m=
| 1 |
| 3 |
∵20°<m<40°,
∴20°<
| 1 |
| 3 |
解得61°<β<121°,
即β的取值范围为61°<β<121°.
点评:本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.也考查了解一元一次不等式组.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
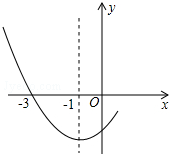 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(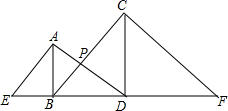 如图,运河边上移栽了两棵老树AB、CD,它们相距20m,分别自两树上高出地面3m、4m的A、C处,向两侧地面上的点E和D、B和F处用绳索拉紧,以固定老树,那么绳索AD与BC的交点P离地面的高度为多少米?
如图,运河边上移栽了两棵老树AB、CD,它们相距20m,分别自两树上高出地面3m、4m的A、C处,向两侧地面上的点E和D、B和F处用绳索拉紧,以固定老树,那么绳索AD与BC的交点P离地面的高度为多少米?