题目内容
10.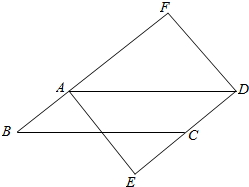 如图,在?ABCD中,过点A作AE⊥DC交DC的延长线于点E过点D作DF⊥BA,交BA的延长线于点F.
如图,在?ABCD中,过点A作AE⊥DC交DC的延长线于点E过点D作DF⊥BA,交BA的延长线于点F.(1)求证:四边形AEDF是矩形;
(2)连接BD,若AB=AE=2,tan∠FAD=$\frac{2}{5}$,求BD的长.
分析 (1)由四边形ABCD是平行四边形,AE⊥DC,DF⊥BA,易证得四边形AEDF是平行四边形,继而证得四边形AEDF是矩形;
(2)由四边形AEDF是矩形,可得在Rt△AFD中,tan∠FAD=$\frac{FD}{AF}$=$\frac{2}{5}$,继而求得BF的长,然后由勾股定理求得答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AF∥ED,
∵AE⊥DC,DF⊥BA,
∴DF∥EA,
∴四边形AEDF是平行四边形,
∵AE⊥DE,
∴∠E=90°,
∴四边形AEDF是矩形;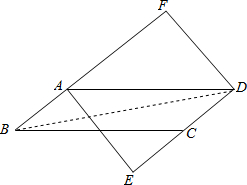 (2)如图,连接BD,
(2)如图,连接BD,
∵四边形AEDF是矩形,
∴FD=AE=2,∠F=90°,
∵在Rt△AFD中,tan∠FAD=$\frac{FD}{AF}$=$\frac{2}{5}$,
∵AF=5,
∴AB=2,
∴BF=AB+AF=7,
在Rt△BFD中,BD=$\sqrt{B{F}^{2}+F{D}^{2}}$=$\sqrt{53}$.
点评 此题考查了平行四边形的性质、矩形的判定与性质、勾股定理以及三角函数等知识.注意利用三角函数,求得AB的长是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.下列事件中是确定事件的为( )
| A. | 两条线段可以组成一个三角形 | |
| B. | 打开电视机正在播放动画片 | |
| C. | 车辆随机经过一个路口,遇到绿灯 | |
| D. | 掷一枚均匀的骰子,掷出的点数是奇数 |
15.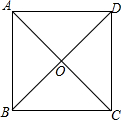 如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
 如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )
如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是( )| A. | AO=BO=CO=DO,AC⊥BD | B. | AC=BC=CD=DA | ||
| C. | AO=CO,BO=DO,AC⊥BD | D. | AB=BC,CD⊥DA |
 已知直线m,n之间的距离是3,△ABC的顶点A在直线m上,边BC在直线n上,求△ABC的面积S和BC边的长x之间的关系式,并指出其中的变量和常量.
已知直线m,n之间的距离是3,△ABC的顶点A在直线m上,边BC在直线n上,求△ABC的面积S和BC边的长x之间的关系式,并指出其中的变量和常量.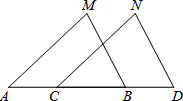 已知:点 A、C、B、D在同一条直线,∠M=∠N,AM=CN.请你添加一个条件,使△ABM≌△CDN,并给出证明.
已知:点 A、C、B、D在同一条直线,∠M=∠N,AM=CN.请你添加一个条件,使△ABM≌△CDN,并给出证明.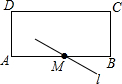 如图所示,在矩形ABCD中,AD=4cm,AB=10cm,点M是AB边上的中点,将点A沿着过点M的直线l翻折使点A落在DC边上,点A的对称点为点P,则PD=2cm或8cm.
如图所示,在矩形ABCD中,AD=4cm,AB=10cm,点M是AB边上的中点,将点A沿着过点M的直线l翻折使点A落在DC边上,点A的对称点为点P,则PD=2cm或8cm.