题目内容
18.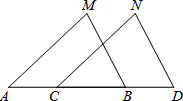 已知:点 A、C、B、D在同一条直线,∠M=∠N,AM=CN.请你添加一个条件,使△ABM≌△CDN,并给出证明.
已知:点 A、C、B、D在同一条直线,∠M=∠N,AM=CN.请你添加一个条件,使△ABM≌△CDN,并给出证明.(1)你添加的条件是:∠MAB=∠NCD;
(2)证明:在△ABM和△CDN中
∵∠M=∠N,AM=CM,∠MAB=∠NCD
∴△ABM≌△CDN(ASA)..
分析 判定两个三角形全等的一般方法有:ASA、SSS、SAS、AAS、HL,所以可添加条件为∠MAB=∠NCD,或BM=DN或∠ABM=∠CDN.
解答 解:(1)你添加的条件是:①∠MAB=∠NCD;
(2)证明:在△ABM和△CDN中
∵∠M=∠N,AM=CM,∠MAB=∠NCD
∴△ABM≌△CDN(ASA),
故答案为:∠MAB=∠NCD;
在△ABM和△CDN中
∵∠M=∠N,AM=CM,∠MAB=∠NCD
∴△ABM≌△CDN(ASA).
点评 本题考查三角形全等的性质和判定方法,判定两个三角形全等的一般方法有:ASA、SSS、SAS、AAS、HL(在直角三角形中).判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
3.已知点P(a,b)满足ab<0,a-b>0,则点P在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.下列事件中是必然事件的是( )
| A. | 打开电视机,正在播无棣新闻 | |
| B. | 今年春节,我们县的天气一定是晴天 | |
| C. | “大衣哥”朱之文一定能上2016年春节联欢晚会 | |
| D. | 从一个只装有红球的箱子里摸出一个球,摸出的球是红球 |
 如图,小正方形的边长为1,则图中三角形(阴影部分)与△ABC相似的是( )
如图,小正方形的边长为1,则图中三角形(阴影部分)与△ABC相似的是( )



 如图,在?ABCD中,过点A作AE⊥DC交DC的延长线于点E过点D作DF⊥BA,交BA的延长线于点F.
如图,在?ABCD中,过点A作AE⊥DC交DC的延长线于点E过点D作DF⊥BA,交BA的延长线于点F.