题目内容
19.适合下列条件的△ABC中,是直角三角形的有个( )①a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$②∠A=32°,∠B=58°③a=7,b=24,c=25.④a:b:c=1:1:2⑤b2=a2-c2.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据勾股定理的逆定理即可判断①③④;求出∠C的度数,即可判断②.
解答 解:∵a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$,
∴a2+b2≠c2,
∴此时三角形不是直角三角形,∴①错误;
∵∠A=32°,∠B=58°,
∴∠C=180°-∠A-∠B=90°,
∴此时三角形是直角三角形,∴②正确;
∵a=7,b=24,c=25,
∴a2+b2=c2,
∴此时三角形是直角三角形,∴③正确;
∵a:b:c=1:1:2,
∴a2+b2=c2,
∴此时三角形是直角三角形,∴④正确;
∵b2=a2-c2,
∴b2+c2=a2,
∴此时三角形是直角三角形,∴⑤正确;
即直角三角形共4个.
故选C.
点评 本题考查了勾股定理的逆定理和三角形内角和定理的应用,能熟记勾股定理的逆定理内容是解此题的关键.

练习册系列答案
相关题目
7.下列事件中是必然事件的是( )
| A. | 打开电视机,正在播无棣新闻 | |
| B. | 今年春节,我们县的天气一定是晴天 | |
| C. | “大衣哥”朱之文一定能上2016年春节联欢晚会 | |
| D. | 从一个只装有红球的箱子里摸出一个球,摸出的球是红球 |
14.单项式-$\frac{{a}^{2}b}{7}$的系数和次数分别是( )
| A. | -7,2 | B. | -$\frac{1}{7}$,2 | C. | -$\frac{1}{7}$,3 | D. | $\frac{1}{7}$,3 |
9.下列图形选自历届世博会会徽,其中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
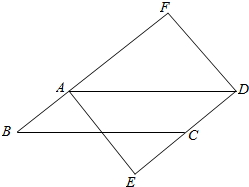 如图,在?ABCD中,过点A作AE⊥DC交DC的延长线于点E过点D作DF⊥BA,交BA的延长线于点F.
如图,在?ABCD中,过点A作AE⊥DC交DC的延长线于点E过点D作DF⊥BA,交BA的延长线于点F.