题目内容
5.在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则关于点D的说法正确的是( )甲:点D在第一象限
乙:点D与点A关于原点对称
丙:点D的坐标是(-2,1)
丁:点D与原点距离是$\sqrt{5}$.
| A. | 甲乙 | B. | 丙丁 | C. | 甲丁 | D. | 乙丙 |
分析 由点的坐标特征得出点A和点C关于原点对称,由平行四边形的性质得出D和B关于原点对称,即可得出点D的坐标,再由勾股定理求出即可.
解答 解:∵A(m,n),C(-m,-n),
∴点A和点C关于原点对称,
∵四边形ABCD是平行四边形,
∴D和B关于原点对称,
∵B(2,-1),
∴点D的坐标是(-2,1),
∴点D到原点的距离=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$.
故选:B.
点评 本题考查了平行四边形的性质、关于原点对称的点的坐标特征、勾股定理;熟练掌握平行四边形的性质,得出D和B关于原点对称是解决问题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
20.计算|-6|-(-$\frac{1}{3}$)0的值是( )
| A. | 5 | B. | -5 | C. | 5$\frac{2}{3}$ | D. | 7 |
 一次函数y=kx+b(k,b为常数,k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=3的解为x=2.
一次函数y=kx+b(k,b为常数,k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=3的解为x=2.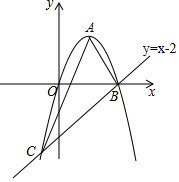 如图,已知抛物线y=-x2+2x经过原点O,且与直线y=x-2交于B,C两点.
如图,已知抛物线y=-x2+2x经过原点O,且与直线y=x-2交于B,C两点.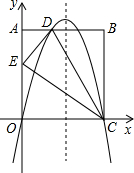 如图,在矩形ABCD中,AO=10,AB=8,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,点D(3,10)、E(0,6),抛物线y=ax2+bx+c经过O,D,C三点.
如图,在矩形ABCD中,AO=10,AB=8,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,点D(3,10)、E(0,6),抛物线y=ax2+bx+c经过O,D,C三点.