Question

2．图中，ABCD为一梯形，其中AB∥CD，AC=BD．
（1）∠ABD是否等于∠BAC？试解释你的答案；
（2）求∠CAB．

Answer 1

分析 （1）结论：∠ABD=∠CAB．只要证明△ACE≌△BDF即可解决问题；
（2）利用平行线的性质求出∠B即可解决问题；

解答 解：（1）结论：∠ABD=∠CAB．理由如下：
如图，作CE⊥AB于E，DF⊥AB于F．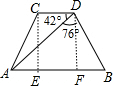
∵AB∥CD，
∴CE=DF，
在Rt△ACE和Rt△BDF中，
$\left\{\begin{array}{l}{AC=BD}\\{CE=DF}\end{array}\right.$，
∴△ACE≌△BDF，
∴∠ABD=∠CAB．

（2）∴CD∥AB，
∴∠B+∠CDB=180°，
∵∠CDB=∠CDA+∠ADB=118°，
∴∠CAB=∠B=62°．

点评 本题考查梯形的性质，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．