题目内容
12．
如图，在边长为1的正方形ABCD中，点A的坐标为（1，1），AD∥x轴，动点P沿B→A→D→C→B运动，以点P为顶点的抛物线y=ax2+bx+c（a≠0）交x轴于M、N两点（点M在点N的左边），当点P运动时，该抛物线随之平移．若点M的横坐标的最小值为-1，则点N的横坐标的最大值为4．
分析 由当顶点P在BA上运动时，点M的横坐标取得最小值-1，结合点A的坐标得出抛物线的对称轴x=1，即可知点M、N的距离为4，再由顶点P在线段CD上运动时，点N的横坐标取得最大值可得答案．
解答 解：当顶点P在BA上运动时，点M的横坐标最小为-1，
∵点A的坐标为（1，1），
∴抛物线的对称轴为x=1，
则此时抛物线与x轴的另一个交点N的横坐标为3，
当顶点P在线段CD上运动时，点N的横坐标取得最大值，最大值为4，
故答案为：4．
点评 本题主要考查抛物线与x轴的交点，熟练掌握二次函数的图象和性质、正方形的性质、平移的性质是解题的关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
图中，ABCD为一梯形，其中AB∥CD，AC=BD．
20．某电视台的娱乐节目《周末大放送》有这样的翻奖牌游戏：如图所示，将一个正方形均分成9等份，数字的背面写有祝福语或奖金数．游戏规则是：每次翻动正面一个数字，看看反面对应的内容，就可知是得奖还是得到温馨祝福
正面 反面
请你完成下列问题：
（1）翻到奖金1000元的概率是多少？
（2）翻不到奖金的概率是多少？
（3）一选手准备在奇数中选择一个数字，他获得奖金的概率是多少？
正面 反面
| 1 | 2 | 3 | 祝你开心 | 万事如意 | 奖金1000元 | |
| 4 | 5 | 6 | 身体健康 | 心想事成 | 奖金500元 | |
| 7 | 8 | 9 | 奖金100元 | 生活愉快 | 谢谢参与 |
（1）翻到奖金1000元的概率是多少？
（2）翻不到奖金的概率是多少？
（3）一选手准备在奇数中选择一个数字，他获得奖金的概率是多少？
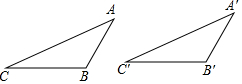如图，∠B=∠B′＞90°，AB=A′B′，AC=A′C′．求证：△ABC≌△A′B′C′．
