题目内容
13.P为正△ABC内一点,PD、PE、PF分别垂直△ABC各边,D、E、F分别为垂足,若PD=1,PE=2,PF=3,则△ABC的面积为12$\sqrt{3}$.分析 连接AP、BP、CP,设等边三角形的边长为x,根据等边三角形的性质结合三角形的面积即可得出关于x的一元二次方程,解之取其正值即可得出等边三角形的边长,再将其代入S△ABC=3x即可得出结论.
解答 解:连接AP、BP、CP,如图所示.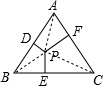
设等边三角形的边长为x,
则S△ABC=$\frac{1}{2}$x•$\frac{\sqrt{3}}{2}$x=$\frac{1}{2}$x•1+$\frac{1}{2}$x•2+$\frac{1}{2}$x•3,
即$\frac{\sqrt{3}}{4}$x2=3x,
解得:x1=0(舍去),x2=4$\sqrt{3}$,
∴S△ABC=3x=12$\sqrt{3}$.
故答案为:12$\sqrt{3}$.
点评 本题考查了等边三角形的性质.三角形的面积以及解一元二次方程,根据等边三角形的性质结合三角形的面积找出关于x的一元二次方程是解题的关键.

练习册系列答案
相关题目
1.下列运算中,错误的是( )
| A. | $\frac{x-y}{x+y}$=-$\frac{y-x}{y+x}$ | B. | $\frac{-a-b}{a+b}$=-1 | C. | $\sqrt{{(1-\sqrt{2})}^{2}}$=$\sqrt{2}$-1 | D. | $\sqrt{{a}^{2}}$=a |
18.为了了解湖州市2017年中考数学学科各分数段成绩分布情况,从中抽取2000名考生的中考数学成绩进行统计分析,在这个问题中,样本是指( )
| A. | 2000 | |
| B. | 湖州市2017年中考数学成绩 | |
| C. | 被抽取的2000名考生 | |
| D. | 被抽取的2000名考生的中考数学成绩 |
5.已知x>y,则-3x+5( )-3y+5,那么括号里应填入( )
| A. | = | B. | > | C. | < | D. | 不能确定 |
 图中,ABCD为一梯形,其中AB∥CD,AC=BD.
图中,ABCD为一梯形,其中AB∥CD,AC=BD.