题目内容
15.如图,Rt△ABC和Rt△DEC如图①叠放在一起,AB=DE=4,AC=DC=5,将△DEC绕点C顺时针旋转.(1)如图②,当点E所经过的路径长为$\frac{π}{2}$时,求旋转角的度数;
(2)如图③,当点E恰好落在AC边上时,求△BEC的面积.

分析 (1)在Rt△ABC中根据勾股定理得到BC=3,再利用旋转的性质得CE=CB=3,∠BCE等于旋转角,设∠BCE=n°,则根据弧长公式得到$\frac{n•π•3}{180}$=$\frac{π}{2}$,解得n=30,于是得到旋转角的度数为30°;
(2)作EH⊥BC于H,如图③,证明△CEH∽△CAB,利用相似比计算出EH=$\frac{12}{5}$,然后根据三角形面积公式求解.
解答 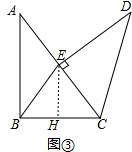 解:(1)在Rt△ABC中,∵AB=4,AC=5,
解:(1)在Rt△ABC中,∵AB=4,AC=5,
∴BC=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∵△DEC绕点C顺时针旋转,
∴CE=CB=3,∠BCE等于旋转角,
设∠BCE=n°,
∴$\frac{n•π•3}{180}$=$\frac{π}{2}$,解得n=30,
∴旋转角的度数为30°;
(2)作EH⊥BC于H,如图③,
∵EH∥AB,
∴△CEH∽△CAB,
∴$\frac{EH}{AB}$=$\frac{CE}{CA}$,即$\frac{EH}{4}$=$\frac{3}{5}$,解得EH=$\frac{12}{5}$,
∴S△BEC=$\frac{1}{2}$•BC•EH=$\frac{1}{2}$×3×$\frac{12}{5}$=$\frac{18}{5}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理和相似三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.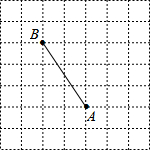 在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )
在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )
 在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )
在7×7的方格中,每个小方格的边长均为1,A、B两点都在格点上,若在格点上找到一点P,使△PAB的面积为6,则符合条件的点P有( )| A. | 2个 | B. | 4个 | C. | 8个 | D. | 12个 |
6.观察下列球的排列规律(其中●是实心球,○是空心球):
●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●…
从第1个球起到第2012个球止,共有实心球的个数为( )
●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●…
从第1个球起到第2012个球止,共有实心球的个数为( )
| A. | 598 | B. | 602 | C. | 604 | D. | 608 |
3. 菏泽牡丹博览会国花馆展厅志愿者的年龄分布如图,这些志愿者年龄的中位数和众数分别是( )
菏泽牡丹博览会国花馆展厅志愿者的年龄分布如图,这些志愿者年龄的中位数和众数分别是( )
 菏泽牡丹博览会国花馆展厅志愿者的年龄分布如图,这些志愿者年龄的中位数和众数分别是( )
菏泽牡丹博览会国花馆展厅志愿者的年龄分布如图,这些志愿者年龄的中位数和众数分别是( )| A. | 20岁,19岁 | B. | 20岁,20岁 | C. | 21岁,20岁 | D. | 22岁,20岁 |
7.一次函数y=5x-2013的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.以下关于二次函数y=2(x+2)2+7的说法正确的是( )
| A. | 开口向下 | B. | 对称轴是直线x=2 | C. | 最小值是-7 | D. | 最大值是-7 |
5.下表列出了几个国外城市与北京的时差(带正号的数表示同一时刻比北京时间晚的时数):例如:在卡塔尔首都多哈举行的第15届亚运会开幕式是在北京时间17:00开始进行的,而此时东京时间是18:00.
①如果现在是北京时间9:00,那么纽约时间是多少?
②如果现在小东在北京想给远在巴黎的姨妈打电话,你认为是否合适,为什么?
③2001年9月11日上午9时许(纽约时间),美国纽约世贸中心姊妹楼先后分别遭恐怖分子劫持的两架飞机的袭击,此时北京是什么时候?
| 城市 | 时差(时) |
| 纽约 | -13 |
| 巴黎 | -7 |
| 东京 | +1 |
②如果现在小东在北京想给远在巴黎的姨妈打电话,你认为是否合适,为什么?
③2001年9月11日上午9时许(纽约时间),美国纽约世贸中心姊妹楼先后分别遭恐怖分子劫持的两架飞机的袭击,此时北京是什么时候?
 如图,在直角△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB=75°.
如图,在直角△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB=75°.