题目内容
5.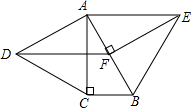 如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$时,四边形ADFE是平行四边形.
如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$时,四边形ADFE是平行四边形.
分析 由三角形ABE为等边三角形,EF垂直于AB,利用三线合一得到EF为角平分线,得到∠AEF=30°,进而确定∠BAC=∠AEF,再由一对直角相等,及AE=AB,利用AAS即可得证△ABC≌△EAF;由∠BAC与∠DAC度数之和为90°,得到DA垂直于AB,而EF垂直于AB,得到EF与AD平行,再由全等得到EF=AC,而AC=AD,可得出一组对边平行且相等,即可得证.
解答 解:当$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$时,四边形ADFE是平行四边形.
理由:∵$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$,
∴∠CAB=30°,
∵△ABE为等边三角形,EF⊥AB,
∴EF为∠BEA的平分线,∠AEB=60°,AE=AB,
∴∠FEA=30°,又∠BAC=30°,
∴∠FEA=∠BAC,
在△ABC和△EAF中,
$\left\{\begin{array}{l}{∠ACB=∠EFA}\\{∠BAC=∠AEF}\\{AB=AE}\end{array}\right.$,
∴△ABC≌△EAF(AAS);
∵∠BAC=30°,∠DAC=60°,
∴∠DAB=90°,即DA⊥AB,
∵EF⊥AB,
∴AD∥EF,
∵△ABC≌△EAF,
∴EF=AC=AD,
∴四边形ADFE是平行四边形.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 此题考查了平行四边形的判定、平行线的判定与性质、全等三角形的判定与性质以及等边三角形的性质,熟练掌握判定与性质是解本题的关键.

练习册系列答案
相关题目
13.解不等式2x≥x-1,并把解集在数轴上表示( )
| A. |  | B. |  | C. |  | D. |  |
10. 如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )
 如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠A=70°,则∠C的度数是( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
17.下列运算中正确的是( )
| A. | a3-a2=a | B. | a3•a4=a12 | C. | a6÷a2=a3 | D. | (-a2)3=-a6 |
15.将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数3相差2的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
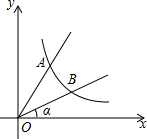 如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=$\frac{1}{2}$.
如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=$\frac{1}{2}$.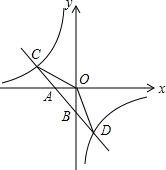 如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=$\frac{{k}_{2}}{x}$的图象分别交于C、D两点,点D(2,-3),点B是线段AD的中点.
如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=$\frac{{k}_{2}}{x}$的图象分别交于C、D两点,点D(2,-3),点B是线段AD的中点.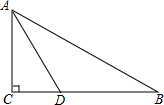 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=2.
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=2.