题目内容
15.将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数3相差2的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
分析 由一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数,掷一次这枚骰子,向上的一面的点数为与点数3相差2的有2种情况,直接利用概率公式求解即可求得答案.
解答 解:∵一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数,掷一次这枚骰子,向上的一面的点数为点数3相差2的有2种情况,
∴掷一次这枚骰子,向上的一面的点数为点数3相差2的概率是:$\frac{2}{6}$=$\frac{1}{3}$.
故选B.
点评 此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
3.下列运算结果,错误的是( )
| A. | -(-$\frac{1}{2}$)=$\frac{1}{2}$ | B. | (-1)0=1 | C. | (-1)+(-3)=4 | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
10.计算:3-2×(-1)=( )
| A. | 5 | B. | 1 | C. | -1 | D. | 6 |
20.分式$\frac{1}{x-1}$有意义,则x的取值范围是( )
| A. | x>1 | B. | x≠1 | C. | x<1 | D. | 一切实数 |
7.在排球训练中,甲、乙、丙三人相互传球,由甲开始发球(记作为第一次传球),则经过三次传球后,球仍回到甲手中的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
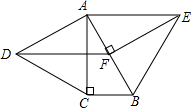 如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$时,四边形ADFE是平行四边形.
如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$时,四边形ADFE是平行四边形.