题目内容
10.已知mx-n<0的解集为x>$\frac{1}{7}$,则nx-m>0的解集是x<7.分析 第一个不等式的方向改变,说明不等式两边除以的m小于0,由解集是x>$\frac{1}{7}$,可以继续判断n的符号;就可以得到第二个不等式的解集.
解答 解:由mx-n<0的解集为x>$\frac{1}{7}$,不等号方向改变,
∴m<0且$\frac{n}{m}$=$\frac{1}{7}$>0,
∴n<0;
由nx-m>0得x<$\frac{m}{n}$=7,
所以x<7;
故答案为<7.
点评 本题考查了解一元一次不等式组和不等式的性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.某班10名学生校服尺寸与对应人数如下表所示:
则这10名学生校服尺寸的众数和中位数分别为( )
| 尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
| 学生人数(人) | 1 | 3 | 2 | 2 | 2 |
| A. | 165,165 | B. | 165,170 | C. | 170,165 | D. | 170,170 |
20.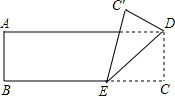 如图,将一张矩形纸片ABCD折叠,使顶点C落在C′处,测量得AB=4,DE=8,则sin∠C′ED为( )
如图,将一张矩形纸片ABCD折叠,使顶点C落在C′处,测量得AB=4,DE=8,则sin∠C′ED为( )
 如图,将一张矩形纸片ABCD折叠,使顶点C落在C′处,测量得AB=4,DE=8,则sin∠C′ED为( )
如图,将一张矩形纸片ABCD折叠,使顶点C落在C′处,测量得AB=4,DE=8,则sin∠C′ED为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
 如图,△ABD与△ACE均为等腰直角三角形且摆成如图所示的样子,若∠ABC=90°(图中所有的点、线都在同一平面内),DF=$\sqrt{2}$,EF=2$\sqrt{2}$,则线段BC的长为$\sqrt{7}$-1.
如图,△ABD与△ACE均为等腰直角三角形且摆成如图所示的样子,若∠ABC=90°(图中所有的点、线都在同一平面内),DF=$\sqrt{2}$,EF=2$\sqrt{2}$,则线段BC的长为$\sqrt{7}$-1. 如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )
如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )


