题目内容
5. 如图,△ABD与△ACE均为等腰直角三角形且摆成如图所示的样子,若∠ABC=90°(图中所有的点、线都在同一平面内),DF=$\sqrt{2}$,EF=2$\sqrt{2}$,则线段BC的长为$\sqrt{7}$-1.
如图,△ABD与△ACE均为等腰直角三角形且摆成如图所示的样子,若∠ABC=90°(图中所有的点、线都在同一平面内),DF=$\sqrt{2}$,EF=2$\sqrt{2}$,则线段BC的长为$\sqrt{7}$-1.
分析 作FG⊥AD于G.首先证明CF⊥AE,推出AF=CF=EF=2$\sqrt{2}$,AC=4,再求出AD,在Rt△ABC中可以求出BC.
解答 解:作FG⊥AD于G.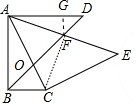
∵∠ABC=90°,∠ABD=45°,
∴∠FBC=45°,∵∠FAC=45°,
∴∠OAF=∠OBC=45°,∵∠AOF=∠BOC,
∴△AOF∽△BOC,
∴∠AFO=∠OCB,$\frac{OA}{OB}$=$\frac{OF}{OC}$,
∴$\frac{OA}{OF}$=$\frac{OB}{OC}$,∵∠AOB=∠COF,
∴△AOB∽△FOC,
∴∠OAB=∠OFC,
∵∠OAB+∠OCB=90°,
∴∠AFO+∠OFC=90°,
∴CF⊥AE,∴CA=CE,∠ACE=90°,
∴CF=AF=EF=2$\sqrt{2}$,
在Rt△FGD中,∵DF=$\sqrt{2}$,∠D=45°,
∴FG=DG=1,
∴AG=$\sqrt{A{F}^{2}-G{F}^{2}}$=$\sqrt{8-1}$=$\sqrt{7}$,
∴AB=AD=$\sqrt{7}$+1,
在Rt△ACB中,BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{4}^{2}-(\sqrt{7}+1)^{2}}$=$\sqrt{7}$-1.
故答案为$\sqrt{7}$-1.
点评 本题考查等腰直角三角形的性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,正确寻找相似三角形解决问题,属于中考填空题中的压轴题.

练习册系列答案
相关题目
13. 如图,△ABC三个顶点分别在反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$的图象上,若∠C=90°,AC∥y轴,BC∥x轴,S△ABC=8,则k的值为( )
如图,△ABC三个顶点分别在反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$的图象上,若∠C=90°,AC∥y轴,BC∥x轴,S△ABC=8,则k的值为( )
 如图,△ABC三个顶点分别在反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$的图象上,若∠C=90°,AC∥y轴,BC∥x轴,S△ABC=8,则k的值为( )
如图,△ABC三个顶点分别在反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$的图象上,若∠C=90°,AC∥y轴,BC∥x轴,S△ABC=8,则k的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
16.下列各点中在抛物线y=x2+2x+3的点是( )
| A. | (-2,-5) | B. | (-1,0) | C. | (0,3) | D. | (1,5) |
20. 最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
 最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)| A. | 91.1 | B. | 91.3 | C. | 58.2 | D. | 58.4 |
14.若x<-2是关于x的一元一次不等式ax-2>0的解集,则关于y的方程ay+2=0的解为( )
| A. | y=1 | B. | y=-1 | C. | y=2 | D. | y=-2 |
 如图,灯塔A在港口P的南偏东45°方向,距离港口20$\sqrt{2}$海里处,一艘客轮从港口P出发,沿北偏东30°方向,以20海里/小时的速度驶离港口,客轮出发后几小时后在灯塔的正北方向,并求出此时客轮距灯塔的距离.
如图,灯塔A在港口P的南偏东45°方向,距离港口20$\sqrt{2}$海里处,一艘客轮从港口P出发,沿北偏东30°方向,以20海里/小时的速度驶离港口,客轮出发后几小时后在灯塔的正北方向,并求出此时客轮距灯塔的距离.