题目内容
1.直角三角形ABC中,∠B=90°,AB=5,BC=12,点P为AC线段上的动点,当点P运动时,设PC=x,△ABP的面积为y,则y关于x的表达式为y=-$\frac{30}{13}$x+30.分析 如图,作PD⊥AB,可得△ADP∽△ABC,根据相似三角形的性质,可用x表示出PD的长,根据S△ABP=$\frac{1}{2}$AB×PD,代入数值,即可求出y与x之间的关系式.
解答 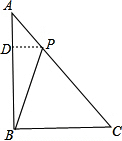 解:∵∠B=90°,AB=5,BC=12,
解:∵∠B=90°,AB=5,BC=12,
∴AC=13,
如图,作PD⊥AB,
∴△ADP∽△ABC,
∴$\frac{PD}{BC}$=$\frac{AP}{AC}$,即$\frac{PD}{12}$=$\frac{13-x}{13}$,
解得,PD=$\frac{156-12x}{13}$,
∴S△ABP=$\frac{1}{2}$AB×PD=$\frac{1}{2}$×5×$\frac{156-12x}{13}$=-$\frac{30}{13}$x+30,
∴y与x之间的关系式为:y=-$\frac{30}{13}$x+30.
故答案为:y=-$\frac{30}{13}$x+30.
点评 本题主要考查了三角形的面积求法和函数关系式,知道三角形的面积计算公式,体会一次函数与二元一次方程的异同点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.正常人红细胞直径平均为0.000 0072米,数字0.000 0072米用科学记数法表示为( )
| A. | 7.2×107 | B. | 0.72×10-6 | C. | 7.2×10-6 | D. | 72×10-7 |
16.下列各点中在抛物线y=x2+2x+3的点是( )
| A. | (-2,-5) | B. | (-1,0) | C. | (0,3) | D. | (1,5) |
11.线段CD是由线段AB平移得到的,点A(4,7)的对应点为C(-1,4),则点B(-4,-1)的对应点D的坐标为( )
| A. | (-9,-4) | B. | (-1,-2) | C. | (2,9) | D. | (5,3) |
 如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )



 如图,∠1=45°,∠D=45°,AB∥CD,则BC与DE有什么位置关系?请说明理由.
如图,∠1=45°,∠D=45°,AB∥CD,则BC与DE有什么位置关系?请说明理由.