题目内容
19.已知关于x的一元二次方程ax2-(3a-2)x+(2a-1)=0,其根的判别式的值为4,求a的值及方程的解.分析 先根据△=4得出a的值,再把a的值代入方程即可得出方程的解.
解答 解:∵一元二次方程ax2-(3a-2)x+(2a-1)=0根的判别式的值为4,
∴△=(3a-2)2-4a(2a-1)=4,
解得a=0或8,
∵ax2-(3a-2)x+(2a-1)=0是一元二次方程,
∴a≠0,
∴a=8,
∴一元二次方程为8x2-22x+15=0,
因式分解得,(2x-3)(4x-5)=0,
解得x1=$\frac{3}{2}$,x2=$\frac{5}{4}$.
点评 本题考查了根的判别式以及一元二次方程的定义,切记不要忽略一元二次方程二次项系数不为零这一隐含条件.

练习册系列答案
相关题目
11.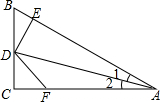 如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )
如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )
 如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )
如图,DC⊥AC于C,DE⊥AB于E,并且DE=DC,则下列结论中正确的是( )| A. | ∠1=∠2 | B. | DE=DF | C. | BD=FD | D. | AB=AC |
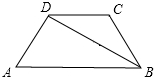 如图,在四边形ABCD中,DC∥AB,对角线BD平分∠ABC,且BD⊥AD,若AD=2,CD=3,则对角线BD的长为4$\sqrt{2}$.
如图,在四边形ABCD中,DC∥AB,对角线BD平分∠ABC,且BD⊥AD,若AD=2,CD=3,则对角线BD的长为4$\sqrt{2}$. 如图,?ABCD中,AE∥CF,AE与BC相交于点P,CF与BD相交于点Q,BP与DQ是否相等,请说明理由.
如图,?ABCD中,AE∥CF,AE与BC相交于点P,CF与BD相交于点Q,BP与DQ是否相等,请说明理由.