题目内容
8.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=x2+2x+m上的三点,则y1,y2,y3的大小关系为y1<y2<y3.
分析 先根据二次函数的性质得到抛物线的对称轴为直线x=-1,然后比较三个点离直线x=-1的远近得到y1、y2、y3的大小关系.
解答 解:∵二次函数的解析式可化为y=(x+1)2+m-1,
∴抛物线的对称轴为直线x=-1,
∵A(-2,y1)、B(1,y2)、C(2,y3),
∴点C离直线x=-1最远,点A离直线x=-1最近,
而抛物线开口向上,
∴y3>y2>y1;
故答案为y3>y2>y1.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.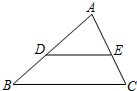 如图,△ABC中,点D、E分别为AB、AC上的点,且满足DE∥BC,若AD=3,BD=2,AE=2,则EC的长为( )
如图,△ABC中,点D、E分别为AB、AC上的点,且满足DE∥BC,若AD=3,BD=2,AE=2,则EC的长为( )
 如图,△ABC中,点D、E分别为AB、AC上的点,且满足DE∥BC,若AD=3,BD=2,AE=2,则EC的长为( )
如图,△ABC中,点D、E分别为AB、AC上的点,且满足DE∥BC,若AD=3,BD=2,AE=2,则EC的长为( )| A. | 3 | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | 1 |
 如图,扇形AOB的面积,占圆O面积的15%,则扇形AOB的圆心角的度数是54°.
如图,扇形AOB的面积,占圆O面积的15%,则扇形AOB的圆心角的度数是54°. 如图,一次函数y=k1x-1的图象经过A(0,-1)、B(1,0)两点,与反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限内的交点为M,若△OBM的面积为1.
如图,一次函数y=k1x-1的图象经过A(0,-1)、B(1,0)两点,与反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限内的交点为M,若△OBM的面积为1. 如图.E,F在线段BC上,AB=DC,BF=CE,∠B=∠C,求证:AF=DE.
如图.E,F在线段BC上,AB=DC,BF=CE,∠B=∠C,求证:AF=DE. 作图:(温馨提醒:确认后,在答题纸上用黑色水笔描黑)
作图:(温馨提醒:确认后,在答题纸上用黑色水笔描黑)