题目内容
13.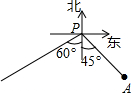 如图,小岛A在港口P的南偏东45°方向、距离港口81海里处.甲船从A出发,沿AP方向以9海里/h的速度驶向港口;乙船从港口P出发,沿南偏西60°方向,以18海里/h的速度驶离港口.现两船同时出发,当甲船在乙船的正东方向时,行驶的时间为9($\sqrt{2}$-1)h.(结果保留根号)
如图,小岛A在港口P的南偏东45°方向、距离港口81海里处.甲船从A出发,沿AP方向以9海里/h的速度驶向港口;乙船从港口P出发,沿南偏西60°方向,以18海里/h的速度驶离港口.现两船同时出发,当甲船在乙船的正东方向时,行驶的时间为9($\sqrt{2}$-1)h.(结果保留根号)
分析 连接AB在P正南方向取点Q,则PQ⊥BA于Q,根据PQ是直角三角形PQB和PQA的公共边,可用时间表示出PB和PA的长,然后根据PQ在不同直角三角形中不同的表达式,来求出时间.
解答 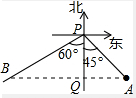 解:设出发t小时后甲船在乙船的正东方向,连接AB在P正南方向取点Q,则PQ⊥BA于Q,
解:设出发t小时后甲船在乙船的正东方向,连接AB在P正南方向取点Q,则PQ⊥BA于Q,
在Rt△PQC中,∠CPB=60°,∴PQ=PBcos60°=$\frac{1}{2}$×18t=9t,
在Rt△PQB中,∠APQ=45°,∴PQ=APcos45°=$\frac{\sqrt{2}}{2}$(81-9t)
则$\frac{\sqrt{2}}{2}$(81-9t)=9t,
解得:t=$\frac{9\sqrt{2}}{2+\sqrt{2}}$=9($\sqrt{2}$-1),
答:当甲船在乙船的正东方向时,行驶的时间为9($\sqrt{2}$-1)h.
故答案为:9($\sqrt{2}$-1).
点评 此题考查了解直角三角形,关键是要构建出与已知条件和问题相关的直角三角形,然后依据公共直角边来求解.

练习册系列答案
相关题目
3.方程x-3=2x-4的解为( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
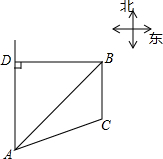 已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)
已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)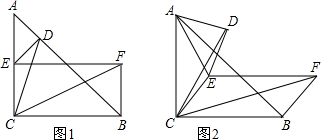
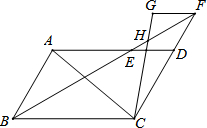 ?ABCD中,∠ABC=60°,∠ABC的角平分线与AD交于点E,交CD延长线于点F,FG∥DA且FG=DE,连接CG,CG与EF交于点H.
?ABCD中,∠ABC=60°,∠ABC的角平分线与AD交于点E,交CD延长线于点F,FG∥DA且FG=DE,连接CG,CG与EF交于点H.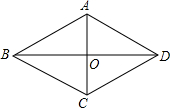 如图,四边形ABCD是菱形,对角线AC、BD相交于O,如果菱形的周长是40cm,它的一条对角线AC长10cm,
如图,四边形ABCD是菱形,对角线AC、BD相交于O,如果菱形的周长是40cm,它的一条对角线AC长10cm,