题目内容
7.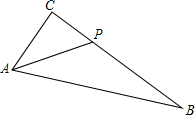 如图.在Rt△ABC中,∠C=90°,AC=6,BC=10.设P为BC上任一点,P点不与BC重合,且CP=x,若y表示△ABP的面积.
如图.在Rt△ABC中,∠C=90°,AC=6,BC=10.设P为BC上任一点,P点不与BC重合,且CP=x,若y表示△ABP的面积.(1)求y与x之间的函数关系式;
(2)自变量x的取值范围.
分析 (1)由图形可知三角形ABP边BP上的高为AC,利用三角形的面积公式表示出y,即可得到y与x之间的函数关系式;
(2)根据关系式结合实际得出自变量的取值范围即可.
解答 解:(1)∵BC=8,CP=x,
∴BP=8-x,
∴S△ABP=$\frac{1}{2}$×BP•AC
=$\frac{1}{2}$×(8-x)×6
=24-3x,
即y=24-3x,
(2)根据题意可得自变量的取值范围为:(0≤x<8).
点评 本题考查了函数与几何知识的综合问题,有些是以函数知识为背景考查几何相关知识,关键是掌握数与形的转化;有些题目是以几何知识为背景,从几何图形中建立函数关系,关键是运用几何知识建立量与量的等式.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
19. 如图,AB是⊙0的直径,点C、D在⊙0上,∠BOD=110°,AD∥OC,则∠AOC=( )
如图,AB是⊙0的直径,点C、D在⊙0上,∠BOD=110°,AD∥OC,则∠AOC=( )
 如图,AB是⊙0的直径,点C、D在⊙0上,∠BOD=110°,AD∥OC,则∠AOC=( )
如图,AB是⊙0的直径,点C、D在⊙0上,∠BOD=110°,AD∥OC,则∠AOC=( )| A. | 70° | B. | 60° | C. | 50° | D. | 55° |
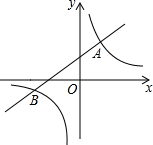 如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象相交于A(2,3),B(-3,n)两点.
如图,一次函数y=kx+b与反比例函数$y=\frac{m}{x}$的图象相交于A(2,3),B(-3,n)两点.