题目内容
3.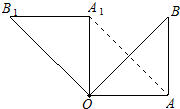 如图,在Rt△OAB,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.连结AA1
如图,在Rt△OAB,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.连结AA1(1)求证:四边形OAA1B1是平行四边形;
(2)求线段AB扫过的面积.
分析 (1)根据旋转的性质得∠AOA1=90°,∠OA1B1=∠OAB=90°,OA=AB=OA1=A1B1,则可判断OA∥A1B1,然后根据平行四边形的判定方法即可得到结论;
(2)如图,先利用勾股定理计算出OB=6$\sqrt{2}$,然后根据扇形面积公式,利用线段AB扫过的面积=S扇形BOB1+S△AOB-S扇形AOA1-S△A1OB1=S扇形BOB1-S扇形AOA1进行计算即可.
解答 (1)证明:∵△OAB绕点O沿逆时针方向旋转90°得到△OA1B1,
∴∠AOA1=90°,∠OA1B1=∠OAB=90°,OA=AB=OA1=A1B1,
∵∠AOA1=∠OA1B1,
∴OA∥A1B1,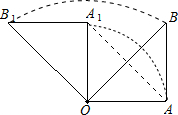
而OA=A1B1,
∴四边形OAA1B1是平行四边形;
(2)如图,
∠OAB=90°,∵OA=AB=6,
∴OB=$\sqrt{2}$OA=6$\sqrt{2}$,
线段AB扫过的面积=S扇形BOB1+S△AOB-S扇形AOA1-S△A1OB1
=S扇形BOB1-S扇形AOA1
=$\frac{90•π•(6\sqrt{2})^{2}}{360}$-$\frac{90•π•{6}^{2}}{360}$
=9π.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的判定与扇形面积公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11. 如图,点A、B、P为⊙O上的点,若∠APB=15°,则∠AOB=( )
如图,点A、B、P为⊙O上的点,若∠APB=15°,则∠AOB=( )
 如图,点A、B、P为⊙O上的点,若∠APB=15°,则∠AOB=( )
如图,点A、B、P为⊙O上的点,若∠APB=15°,则∠AOB=( )| A. | 15° | B. | 20° | C. | 30° | D. | 45° |
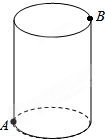 如图,圆柱的高为5cm,底面周长为12cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是$\sqrt{61}$厘米.
如图,圆柱的高为5cm,底面周长为12cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是$\sqrt{61}$厘米.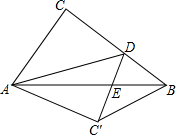 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为$\frac{3}{2}$或$\frac{3}{4}$. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).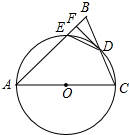 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为点F,连接DE.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为点F,连接DE.