题目内容
14.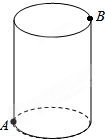 如图,圆柱的高为5cm,底面周长为12cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是$\sqrt{61}$厘米.
如图,圆柱的高为5cm,底面周长为12cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是$\sqrt{61}$厘米.
分析 根据题意得出蚂蚁沿圆柱侧面爬行的最短路程是指展开后线段AB的长,求出AC,BC,根据勾股定理求出AB即可.
解答  解:根据题意得出:蚂蚁沿圆柱侧面爬行的最短路程是指展开后线段AB的长,
解:根据题意得出:蚂蚁沿圆柱侧面爬行的最短路程是指展开后线段AB的长,
由题意得:AC=$\frac{1}{2}$×12=6厘米,BC=5厘米,
由勾股定理得:AB=$\sqrt{{AC}^{2}+{BC}^{2}}$=$\sqrt{{6}^{2}+{5}^{2}}$=$\sqrt{61}$(厘米).
故答案为:$\sqrt{61}$厘米.
点评 本题考查的是平面展开-最短路径问题,根据题意把正方体展开,构造出直角三角形,利用勾股定理进行解答即可.

练习册系列答案
相关题目
9.若x2+8x+m是完全平方式,则m的值等于( )
| A. | 16 | B. | 8 | C. | 4 | D. | 1 |
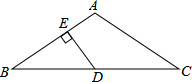 在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足是E,则AE:BE=1:3.
在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足是E,则AE:BE=1:3.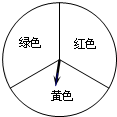 甲、乙两位同学玩转盘游戏,游戏规则:将圆盘平均分成三份,分别涂上红,黄,绿三种颜色,两位同学分别转动转盘两次(若压线,重新转).若两次指针指到的颜色
甲、乙两位同学玩转盘游戏,游戏规则:将圆盘平均分成三份,分别涂上红,黄,绿三种颜色,两位同学分别转动转盘两次(若压线,重新转).若两次指针指到的颜色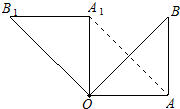 如图,在Rt△OAB,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.连结AA1
如图,在Rt△OAB,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.连结AA1