题目内容
 如图,△ABC的高BD,CE相交于点H,图中与∠A相等的角有
如图,△ABC的高BD,CE相交于点H,图中与∠A相等的角有考点:余角和补角,直角三角形的性质
专题:
分析:由∠A+∠ABD=90°,∠ABD+∠EHB=90°,得出∠A=∠EHB,再由∠EHB=∠DHC,得出∠A=∠EHB=∠DHC;由∠A+∠ABD=90°,∠A+∠ACE=90°,得出与∠A互余的角为∠ABD、∠ACE;由∠EHB+∠BHC=∠EHB+∠EHD=180°,得出与∠A互补的角有∠BHC、∠EHD.
解答:解:∵BD、CE是△ABC的高,
∴∠ADB=∠CDB=90°,∠AEC=∠BEC=90°,
∴∠A+∠ABD=90°,∠ABD+∠EHB=90°,
∴∠A=∠EHB,∵∠EHB=∠DHC,
∴∠A=∠EHB=∠DHC;
∵∠A+∠ACE=90°,
∴与∠A互余的角为∠ABD、∠ACE,
∵∠EHB+∠BHC=∠EHB+∠EHD=180°,
∴∠A+∠BHC=∠A+∠EHD=180°
,即与∠A互补的角有∠BHC、∠EHD;
故答案为:∠EHB、∠DHC;∠ABD、∠ACE;∠BHC、∠EHD.
∴∠ADB=∠CDB=90°,∠AEC=∠BEC=90°,
∴∠A+∠ABD=90°,∠ABD+∠EHB=90°,
∴∠A=∠EHB,∵∠EHB=∠DHC,
∴∠A=∠EHB=∠DHC;
∵∠A+∠ACE=90°,
∴与∠A互余的角为∠ABD、∠ACE,
∵∠EHB+∠BHC=∠EHB+∠EHD=180°,
∴∠A+∠BHC=∠A+∠EHD=180°
,即与∠A互补的角有∠BHC、∠EHD;
故答案为:∠EHB、∠DHC;∠ABD、∠ACE;∠BHC、∠EHD.
点评:本题考查了余角和补角以及直角三角形的两个锐角互余的性质;弄清各个角之间的关系是解题的关键.

练习册系列答案
相关题目
根式①
;②
;③
中,化成最简二次根式后与
的被开方式相同的二次根式的是( )
| 12 |
| 24 |
|
| 6 |
| A、只有② | B、有①③ |
| C、有②③ | D、不存在 |
 画出如图所示的正三棱柱、圆锥的三视图.
画出如图所示的正三棱柱、圆锥的三视图. 如图,直线y=-kx+2与x轴的夹角为30°,与x,y轴的交点分别为A,B.
如图,直线y=-kx+2与x轴的夹角为30°,与x,y轴的交点分别为A,B.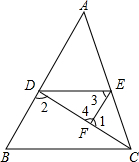 填空:
填空: 如图,在△ABC中,∠C=90°,∠A=30°,DE垂直平分AB交AC于D,交AB于E,若DE=1.5cm,求AC的长.
如图,在△ABC中,∠C=90°,∠A=30°,DE垂直平分AB交AC于D,交AB于E,若DE=1.5cm,求AC的长.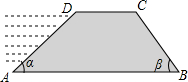 如图,拦水坝的横断面为梯形ABCD,已知上底DC=5m,迎水面坡度为1:
如图,拦水坝的横断面为梯形ABCD,已知上底DC=5m,迎水面坡度为1: