题目内容
 填空:
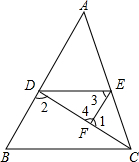
填空:如图所示,已知∠1+∠2=180°,∠3=∠B,求证:∠AED=∠ACB
证明:∵∠1+∠2=180°(已知)
∠1+
∴∠2=
∴AB∥EF(
∴∠3=
∴∠B=
∴DE∥BC(
∴∠AED=∠ACB(
考点:平行线的判定与性质
专题:推理填空题
分析:求出∠2=∠4,根据平行线的判定得出AB∥EF,根据平行线的性质得出∠3=∠ADE,求出∠B=∠ADE,根据平行线的判定得出DE∥BC,根据平行线的性质得出即可.
解答:证明:∵∠1+∠2=180°(已知),∠1+∠4=180°(邻补角定义),
∴∠2=∠4(同角的补角相等),
∴AB∥EF(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠ACB(两直线平行,同位角相等),
故答案为:∠4,∠4,内错角相等,两直线平行,∠ADE,∠ADE,同位角相等,两直线平行,两直线平行,同位角相等.
∴∠2=∠4(同角的补角相等),
∴AB∥EF(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠ACB(两直线平行,同位角相等),
故答案为:∠4,∠4,内错角相等,两直线平行,∠ADE,∠ADE,同位角相等,两直线平行,两直线平行,同位角相等.
点评:本题考查了平行线的性质和判定,补角定义的应用,能运用平行线的性质和判定进行推理是解此题的关键,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
相关题目
下列语句,不是命题的是( )
| A、两点之间线段最短 |
| B、两直线不平行就相交 |
| C、连接A、B两点 |
| D、对顶角相等 |
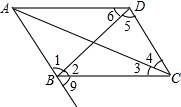 如图,若∠2=∠6,则
如图,若∠2=∠6,则 如图,已知∠1与∠2互补,∠1与∠3相等,那么AB和CD平行吗?EF和CH平行吗?说明理由.
如图,已知∠1与∠2互补,∠1与∠3相等,那么AB和CD平行吗?EF和CH平行吗?说明理由. 如图,直线AB、CD被EF所截,构成8个角,已知∠2=∠6=70°,求∠1、∠3、∠4、∠5、∠7、∠8的度数.
如图,直线AB、CD被EF所截,构成8个角,已知∠2=∠6=70°,求∠1、∠3、∠4、∠5、∠7、∠8的度数. 如图,已知线段AB平移后的位置点C,作出线段AB平移后的图形.
如图,已知线段AB平移后的位置点C,作出线段AB平移后的图形. 如图,△ABC的高BD,CE相交于点H,图中与∠A相等的角有
如图,△ABC的高BD,CE相交于点H,图中与∠A相等的角有