题目内容
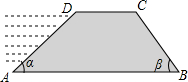 如图,拦水坝的横断面为梯形ABCD,已知上底DC=5m,迎水面坡度为1:
如图,拦水坝的横断面为梯形ABCD,已知上底DC=5m,迎水面坡度为1:| 3 |
(1)坡底AB的长;
(2)迎水坡AD的长.
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:(1)过D点作DE⊥AB于点E,过C作CF⊥AB于点F,分别在△ADE和△BCF中求出AE、BF的长度,然后可求出AB;
(2)根据(1)求得的α的度数利用三角函数求出AD的长度.
(2)根据(1)求得的α的度数利用三角函数求出AD的长度.
解答:解:(1)过D点作DE⊥AB于点E,过C作CF⊥AB于点F.
则四边形DCEF是矩形,有DC=EF=5,DE=CF=4,
∵tana=
=
,
∴AE=4
,α=30°,
∵tanβ=1:1=BF:AF,
∴CF=FB=4,β=45°,
∴AB=AE+EF+BF=(9+4
)米;
(2)∵α=30°,
∴AD=DE÷sin30°=8(米).

则四边形DCEF是矩形,有DC=EF=5,DE=CF=4,
∵tana=
| 1 | ||
|
| ||
| 3 |
∴AE=4
| 3 |
∵tanβ=1:1=BF:AF,
∴CF=FB=4,β=45°,
∴AB=AE+EF+BF=(9+4
| 3 |
(2)∵α=30°,
∴AD=DE÷sin30°=8(米).
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形和矩形,利用锐角三角函数的概念和坡度的概念求解.

练习册系列答案
相关题目
下列语句,不是命题的是( )
| A、两点之间线段最短 |
| B、两直线不平行就相交 |
| C、连接A、B两点 |
| D、对顶角相等 |
 请你试用a,b,c,d表示如图所示的阴影部分的面积S,并求出当a=3,b=5,c=
请你试用a,b,c,d表示如图所示的阴影部分的面积S,并求出当a=3,b=5,c= 如图,直线AB、CD被EF所截,构成8个角,已知∠2=∠6=70°,求∠1、∠3、∠4、∠5、∠7、∠8的度数.
如图,直线AB、CD被EF所截,构成8个角,已知∠2=∠6=70°,求∠1、∠3、∠4、∠5、∠7、∠8的度数. 如图,△ABC的高BD,CE相交于点H,图中与∠A相等的角有
如图,△ABC的高BD,CE相交于点H,图中与∠A相等的角有 如图,在△ABC中,CD⊥AB,垂足为点D,已知AC=4,BC=3,BD=
如图,在△ABC中,CD⊥AB,垂足为点D,已知AC=4,BC=3,BD= 已知AD⊥BC,EF⊥BC,∠1=∠F.求证:AD平分∠BAC.
已知AD⊥BC,EF⊥BC,∠1=∠F.求证:AD平分∠BAC. 已知,如图,AB∥CD,∠BEF与∠EFD的角平分线相交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,证明:PF∥GH.
已知,如图,AB∥CD,∠BEF与∠EFD的角平分线相交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,证明:PF∥GH.