题目内容
3.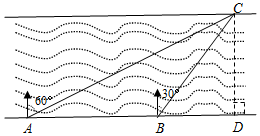 如图,在与南渡江对岸平行的岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,
如图,在与南渡江对岸平行的岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,(1)求∠ACD的度数;
(2)求河宽CD.
分析 (1)在Rt△ACD中,求出∠CAD即可解决问题;
(2)首先由题意可得:∠CAB=90°-60°=30°,∠CBD=90°-30°=60°,AB=200米,CD⊥AB,则可证得△ABC是等腰三角形,即BC=AB,然后在Rt△CBD中,由CD=BC•sin60°,即可求得答案.
解答 解:(1)作CD⊥AB于D.
∵在A点处测得河对岸C点在北偏东60°方向,
∴∠CAD=30°,
∵∠ADC=90°,
∴∠ACD=90°-30°=60°.
(2)根据题意得:∠CAB=90°-60°=30°,∠CBD=90°-30°=60°,AB=200米,CD⊥AB,
则∠ACB=∠CBD-∠CAB=60°-30°=30°,
则BC=AB=200米,
在Rt△CBD中,CD=BC•sin60°=200×$\frac{\sqrt{3}}{2}$=100 $\sqrt{3}$(米).
答:河宽CD为100 $\sqrt{3}$米.
点评 此题考查了方向角问题.此题难度适中,注意能借助于解直角三角形的知识求解是解此题的关键,注意数形结合思想的应用.

练习册系列答案
相关题目
13.设n为正整数,且n-1<$\sqrt{65}$<n,则n的值为( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
18.数据7,-7,0,6,-6,7的中位数和众数分别是( )
| A. | 6,-6 | B. | 3,7 | C. | 0,6 | D. | 0,7 |
8.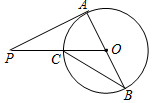 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结BC.若∠P=18°,则∠B等于( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结BC.若∠P=18°,则∠B等于( )
 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结BC.若∠P=18°,则∠B等于( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结BC.若∠P=18°,则∠B等于( )| A. | 27° | B. | 30° | C. | 36° | D. | 54°图3 |
12.经过点(2,-1)作一条直线和反比例函数y=$\frac{2}{x}$相交,当它们有且只有一个公共点时,这样的直线存在( )
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 无数条 |