题目内容
10.如图,⊙O中,弦AB、CD相交点P,弦CA、BD的延长线交于S,∠APD=2m°,∠PAC=m°+15°.(1)求∠S的度数;
(2)连AD,BC,若$\frac{BC}{AD}$=$\sqrt{3}$,求m的值.
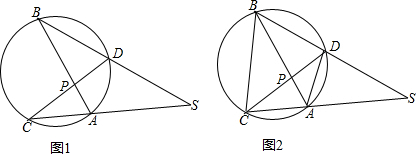
分析 (1)由圆周角定理可知:∠PAC=∠PDB=m°+15°,从而可知∠PDS=∠PAS,由于∠APD=2m°,利用四边形内角和即可得出∠S的度数;
(2)过点C作CE⊥BD于点E,由圆内接四边形的性质可知:∠DAS=∠SBC,从而可证明△SAD∽△SBC,从而可求出ED、CE的长度,从而可得出∠ECD的度数,进而求出m的值.
解答 解:(1)由圆周角定理可知:∠PAC=∠PDB=m°+15°,
∴∠PDS=∠PAS=180-(m°+15°)=165°-m°,
∵∠APD=2m°,
∴∠S=360°-∠PDS-∠PAS-∠APD
=360°-2(165°-m°)-2m°
=30°,
(2)过点C作CE⊥BD于点E,
由圆内接四边形的性质可知:∠DAS=∠SBC,
∵∠S=∠S,
∴△SAD∽△SBC,
∴$\frac{SD}{SC}=\frac{AD}{BC}=\frac{1}{\sqrt{3}}$,
设SD=1,SC=$\sqrt{3}$,
∵∠S=30°,
∴CE=$\frac{1}{2}$SC=$\frac{\sqrt{3}}{2}$,
∴SE=$\sqrt{3}$CE=$\frac{3}{2}$,
∴ED=SE-SD=$\frac{3}{2}$-1=$\frac{1}{2}$,
∴tan∠ECD=$\frac{ED}{CE}=\frac{\sqrt{3}}{3}$,
∴∠ECD=30°,
∴∠EDC=60°,
∴m°+15°=60°,
∴m=45,
点评 本题考查圆的综合问题,涉及相似三角形的性质与判定,圆内接四边形的性质,锐角三角函数等知识,本题属于中等题型.

练习册系列答案
相关题目


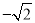 是2的平方根 B.
是2的平方根 B. 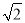 是2的平方根
是2的平方根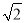 D. 2的算术平方根是
D. 2的算术平方根是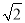
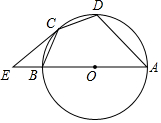 如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,过点C作⊙O的切线交AB的延长线于E,连接BC,CD,AD.
如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,过点C作⊙O的切线交AB的延长线于E,连接BC,CD,AD.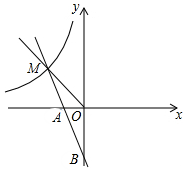 如图,一次函数y=kx+b的图象经过A(-1,0),B(0,-2)l两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第二象限交于点M,△OBM的面积是3.
如图,一次函数y=kx+b的图象经过A(-1,0),B(0,-2)l两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第二象限交于点M,△OBM的面积是3.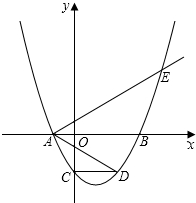 如图,抛物线y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)与x轴分别交于点A(x1,0),B(x2,0)(点A位于点B的左侧),与y轴交于点C(0,-3),
如图,抛物线y=a(x2-2mx-3m2)(其中a,m是常数,且a>0,m>0)与x轴分别交于点A(x1,0),B(x2,0)(点A位于点B的左侧),与y轴交于点C(0,-3),