题目内容
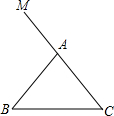如图，在△ABC中，AB=AC，点M在CA的延长线上．（1）实践操作：利用尺规按下列要求作图，并在图中标明相应的字母（不写作法，保留作图痕迹）；
①作∠BAM的平分线AN；
②作AB边上的中线CD，并延长CD交AN于点E；
（2）数学思考：由（1）可得线段AE与边BC的数量关系和位置关系分别是
考点：作图—复杂作图
专题：
分析：（1）利用直尺和圆规即可直接作出；
（2）根据等腰三角形的两底角相等，以及三角形的外角的性质可以证明∠EAB=∠B，则AE∥BC，然后证明△AED≌△BCD即可证得AE=BC．
（2）根据等腰三角形的两底角相等，以及三角形的外角的性质可以证明∠EAB=∠B，则AE∥BC，然后证明△AED≌△BCD即可证得AE=BC．
解答：解：（1）
；
（2）线段AE与边BC的数量关系和位置关系分别是：AE∥BC，且AE=BC．
；（2）线段AE与边BC的数量关系和位置关系分别是：AE∥BC，且AE=BC．
点评：本题考查了尺规作图、等腰三角形的性质以及全等三角形的判定与性质，正确作出图形是关键．
练习册系列答案
名校课堂系列答案
相关题目
如图 已知a∥b，∠1=（175-β）°，∠2=（2β-25）°，求∠1的度数．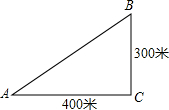
如图，某海滨浴场岸边A处的救生员发现海中B处有人求救，若救生员在岸边行进的速度是8m/s，在海中行进的速度是2m/s，为了节约时间，救生员是直接游向B，还是沿岸边从A处跑到离B最近的点C，然后从点C游向B呢？你能通过计算帮救生员确定营救方案吗？御河中学校团委会要组织一次初三学生篮球联赛，赛制为单循环形式（每两队之间都赛一场），计划安排78场比赛，则参赛球队的个数是（ ）
| A、11个 | B、12个 |
| C、13个 | D、14个 |
已知：△ABC是等边三角形．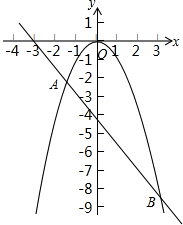
如图所示，抛物线y1=-x2与直线y2=-