题目内容
御河中学校团委会要组织一次初三学生篮球联赛，赛制为单循环形式（每两队之间都赛一场），计划安排78场比赛，则参赛球队的个数是（ ）
| A、11个 | B、12个 |
| C、13个 | D、14个 |
考点：一元二次方程的应用
专题：
分析：赛制为单循环形式（每两队之间都赛一场），x个球队比赛总场数=
，依此即可列方程求解．
| x(x-1) |
| 2 |
解答：解：设有x个队，每个队都要赛（x-1）场，但两队之间只有一场比赛，
x（x-1）÷2=78，
解得x=13或-12（舍去）．
故应邀请13个球队参加比赛．
故选C．
x（x-1）÷2=78，
解得x=13或-12（舍去）．
故应邀请13个球队参加比赛．
故选C．
点评：本题考查了一元二次方程的应用，解决本题的关键是读懂题意，得到总场数的等量关系．
练习册系列答案
同步练习强化拓展系列答案
相关题目
如图所示，P是?ABCD外一点，且AP⊥PC，BP⊥DP，求证：四边形ABCD是矩形．若A=10a2+3b2-5a+5，B=a2+3b2-8a+5，则A-B的值与-9a3b2的公因式为（ ）
| A、a |
| B、-3 |
| C、9a3b2 |
| D、3a |
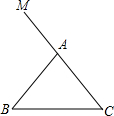如图，在△ABC中，AB=AC，点M在CA的延长线上．
如图，已知△ABC．下列说法中正确的是（ ）
| A、0不是单项式 | ||||
B、
| ||||
C、单项式-
| ||||
D、x-
|
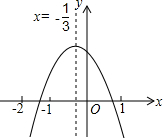如图是二次函数y=ax2+bx+c（a≠0）的图象，有以下结论：