题目内容
 根据二次函数y=x2+3x-4的图象回答:
根据二次函数y=x2+3x-4的图象回答:(1)方程x2+3x-4=0的解是
(2)当
(3)当
考点:抛物线与x轴的交点,二次函数与不等式(组)
专题:
分析:(1)二次函数y=x2+3x-4的图象与x轴的交点横坐标就是方程x2+3x-4=0的解;
(2)看x轴上方图象x的取值范围;
(3)看x轴下方图象x的取值范围.
(2)看x轴上方图象x的取值范围;
(3)看x轴下方图象x的取值范围.
解答:解:由图象可知:
(1)方程x2+3x-4=0的解是x1=-4,x2=1;
(2)当x<-4,或x>1时,y>0;
(3)当-4<x<1时,y<0.
故答案为:x1=-4,x2=1;x<-4,或x>1;-4<x<1.
(1)方程x2+3x-4=0的解是x1=-4,x2=1;
(2)当x<-4,或x>1时,y>0;
(3)当-4<x<1时,y<0.
故答案为:x1=-4,x2=1;x<-4,或x>1;-4<x<1.
点评:此题考查二次函数与x轴的交点问题,主要利用图象研究二次函数与方程、不等式的联系.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
一个正多边形的内角和是900度,则这个多边形是( )
| A、正六边形 | B、正七边形 |
| C、正八边形 | D、正九边形 |
 (2)已知乙车以60km/时的速度匀速行驶,设行驶过程中,两车的距离为s(km),请直接写出s关于x的表达式;
(2)已知乙车以60km/时的速度匀速行驶,设行驶过程中,两车的距离为s(km),请直接写出s关于x的表达式;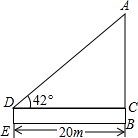 如图,升国旗时,某同学站在离国旗20m处行注目礼,当国旗升至顶端时,该同学视线的仰角为42°,已知双眼离地面1.60m,求旗杆AB的高度(精确到0.01m).
如图,升国旗时,某同学站在离国旗20m处行注目礼,当国旗升至顶端时,该同学视线的仰角为42°,已知双眼离地面1.60m,求旗杆AB的高度(精确到0.01m). 如图,BD是∠ABC的平分线,DE⊥AB,垂足为E,S△ABC=36cm2,AB=18cm,BC=6cm,则DE=
如图,BD是∠ABC的平分线,DE⊥AB,垂足为E,S△ABC=36cm2,AB=18cm,BC=6cm,则DE=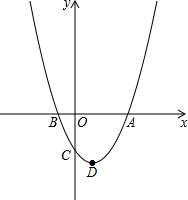 如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.
如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D. 如图,直线yy1=x-1与直线y2=-
如图,直线yy1=x-1与直线y2=- 如图,已知:在△ABC中,点D、E分别在AB、AC上,S△ADE:S△BDE:S△BEC=4:2:3,求证:DE∥BC.
如图,已知:在△ABC中,点D、E分别在AB、AC上,S△ADE:S△BDE:S△BEC=4:2:3,求证:DE∥BC.