题目内容
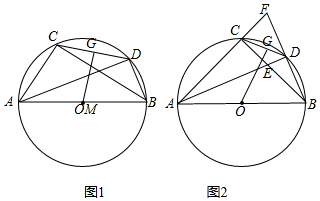
8.如图1,Rt△ABC内接于⊙O,∠ACB=90°,点M为AB中点,点D在弧$\widehat{BC}$上,连接CD、BD,点G是CD的中点,连结MG.(1)求证:MG⊥CD;
(2)如图2,若AC=BC,AD平分∠BAC,AD与BC交于点E,延长BD,与AC的延长线交于点F,求证:CF=CE;
(3)在(2)的条件下,若OG•DE=3(2-$\sqrt{2}$),求⊙O的面积.
分析 (1)根据直角三角形斜边中线的性质,可得OC=OD,利用等腰三角形的性质即可证明;
(2)只要证明△ACE≌△BCF,即可解决问题;
(3)(2)过点O作OH⊥BD于H,根据垂径得BH=DH,则根据三角形中位线性质得AD=2OH,再利用∠CAD=∠BAD得CD=BD,根据弦心距相等,对应的弦相等得到OH=OG,接着证明Rt△BDE∽Rt△ADB,利用相似比得到BD2=AD•DE=2OH•DE=2OG•DE=6(2-$\sqrt{2}$),再利用等腰三角形的判定与性质得DF=BD,AB=AF,即BF=2BD,所以BF2=4BD2=24(2-$\sqrt{2}$),设AC=x,则BC=x,AB=$\sqrt{2}$x=AF,得到CF=AF-AC=( $\sqrt{2}$-1)x,在Rt△BCF中,∵根据勾股定理得[$\sqrt{2}$-1)x]2+x2=24(2-$\sqrt{2}$),解得x=2 $\sqrt{3}$或x=-2 $\sqrt{3}$(舍去),则AB=$\sqrt{2}$x=2 $\sqrt{6}$,于是得到半径OA=$\sqrt{6}$,最后利用圆的面积公式计算即可;
解答 (1)证明:如图1中,
∵∠ACB=90°,
∴AB是⊙O的直径,点M与O重合,
∴∠ADB=90°,
∵OA=OB,
∴CO=$\frac{1}{2}$AB,OD=$\frac{1}{2}$AB,
∴CO=OD,∵CG=GD,
∴CG⊥CD,
即MG⊥CD.
(2)证明:如图2中,
在△ACE和△BCF中,
$\left\{\begin{array}{l}{∠CAE=∠CBE}\\{AC=BC}\\{∠ACE=∠BCF}\end{array}\right.$,
∴△ACE≌△BCF,
∴CE=CF.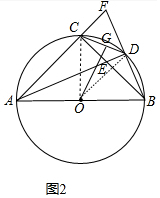
(3)解:过点O作OH⊥BD于H,则BH=DH,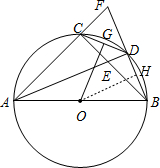
则OH=$\frac{1}{2}$AD,即AD=2OH,
又∵∠CAD=∠BAD,
∴CD=BD,
∴OH=OG,
∵∠DBE=∠DAC=∠BAD,
∴Rt△BDE∽Rt△ADB,
∴BD:AD=DE:BD,
∴BD2=AD•DE=2OH•DE=2OG•DE=6(2-$\sqrt{2}$),
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AD⊥BF,
而AD平分∠BAC,
∴AB=AF,
∴BD=FD,
∴BF=2BD,
∴BF2=4BD2=24(2-$\sqrt{2}$),
设AC=x,则BC=x,AB=$\sqrt{2}$x,
∴AF=$\sqrt{2}$x,
∴CF=AF-AC=$\sqrt{2}$x-x=( $\sqrt{2}$-1)x,
在Rt△BCF中,∵CF2+BC2=BF2,
∴[$\sqrt{2}$-1)x]2+x2=24(2-$\sqrt{2}$),
∴x2=12,解得x=2 $\sqrt{3}$或x=-2 $\sqrt{3}$(舍去),
∴AB=$\sqrt{2}$x=2 $\sqrt{6}$,
∴OA=$\sqrt{6}$,
∴⊙O面积=π•( $\sqrt{6}$)2=6π.
点评 本题考查了圆的综合题、垂径定理、圆周角定理、等腰三角形的判定与性质、勾股定理、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考压轴题.

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案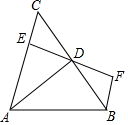 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有( )
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有( )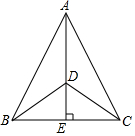 如图,在△ABC中,AB=AC,过点A作AE⊥BC于点E,D为AE上一点,连接DB、DC,∠DBC=α,且$\frac{BD}{AB}$=tanα,记△ABC的面积为S△ABC,△DBC的面积为S△DBC,求$\frac{{S}_{△DBC}}{{S}_{△ABC}}$.
如图,在△ABC中,AB=AC,过点A作AE⊥BC于点E,D为AE上一点,连接DB、DC,∠DBC=α,且$\frac{BD}{AB}$=tanα,记△ABC的面积为S△ABC,△DBC的面积为S△DBC,求$\frac{{S}_{△DBC}}{{S}_{△ABC}}$.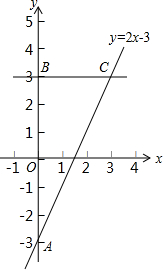 在平面直角坐标系xOy中,直线y=2x-3与y轴交于点A,点A与点B关于x轴对称,过点B作y轴的垂线l,直线l与直线y=2x-3交于点C.
在平面直角坐标系xOy中,直线y=2x-3与y轴交于点A,点A与点B关于x轴对称,过点B作y轴的垂线l,直线l与直线y=2x-3交于点C.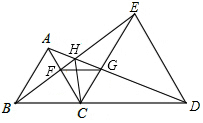 已知,点C是线段BD上一动点,分别以BC、CD为边向同侧作等边△ABC和等边三角形△CDE,如图所示.
已知,点C是线段BD上一动点,分别以BC、CD为边向同侧作等边△ABC和等边三角形△CDE,如图所示.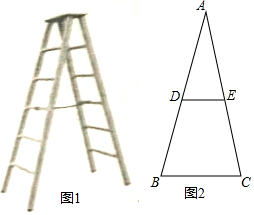 如图1所示的是由梯子AB和梯子AC搭成的“人字梯”,它的5个踩档把梯子等分成6份,梯子的第三踩档处有一条绑绳DE,将其抽象成图2,其中AB=AC=2米.
如图1所示的是由梯子AB和梯子AC搭成的“人字梯”,它的5个踩档把梯子等分成6份,梯子的第三踩档处有一条绑绳DE,将其抽象成图2,其中AB=AC=2米.