题目内容
1.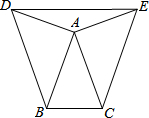 如图,已知AD=AE,∠BDE=∠CED,∠ABD=∠ACE.
如图,已知AD=AE,∠BDE=∠CED,∠ABD=∠ACE.(1)求证:AB=AC;
(2)若∠DAE=2∠ABC=140°,求∠BAD的度数.
分析 (1)由等腰三角形的性质可知∠ADE=∠AED,从而可得到∠ADB=∠AEC,依据AAS可证明△ADB≌△AEC;
(2)由题意可知:∠ABC=70°,由等腰三角形的性质可知∠ABC=∠ACB=70°,由三角形内角和定理可知∠BAC=40°,由△ADB≌△AEC可知∠DAB=∠EAC,故此∠BAD=$\frac{1}{2}$(360°-140°-40°)=90°.
解答 (1)证明:∵AD=AE,
∴∠ADE=∠AED.
∵∠BDE=∠CED,
∴∠BDE-∠ADE=∠CED-∠AED.
∴∠ADB=∠AEC.
在△ADB和△AEC中,
$\left\{\begin{array}{l}{∠ADB=∠AEC\\;}\\{∠ABD=∠ACE}\\{AD=AE}\end{array}\right.$
∴△ADB≌△AEC.
∴AB=AC.
(2)解:∵2∠ABC=140°,
∴∠ABC=70°.
∵AB=AC,
∴∠ABC=∠ACB=70°.
∴∠BAC=180°-∠ABC-∠ACB=40°.
∵△ADB≌△AEC,
∴∠DAB=∠EAC.
∵∠DAE=140°,
∴∠BAD=$\frac{1}{2}$(360°-140°-40°)=90°.
点评 本题主要考查的是全等三角形的性质和判定、等腰三角形的性质,证得△ADB≌△AEC是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12. 如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列三个判断中,①当x>0时,y>0;②若a=-1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;正确的是( )
如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列三个判断中,①当x>0时,y>0;②若a=-1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;正确的是( )
 如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列三个判断中,①当x>0时,y>0;②若a=-1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;正确的是( )
如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列三个判断中,①当x>0时,y>0;②若a=-1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;正确的是( )| A. | ① | B. | ② | C. | ③ | D. | ①②③都不对 |
6. 如图,图中的长方形共有( )个.
如图,图中的长方形共有( )个.
 如图,图中的长方形共有( )个.
如图,图中的长方形共有( )个.| A. | 9 | B. | 8 | C. | 5 | D. | 4 |