题目内容
12. 如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列三个判断中,①当x>0时,y>0;②若a=-1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;正确的是( )
如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列三个判断中,①当x>0时,y>0;②若a=-1,则b=4;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;正确的是( )| A. | ① | B. | ② | C. | ③ | D. | ①②③都不对 |
分析 观察函数图象可直接得到抛物线在x轴上方所对应的自变量的范围,从而可对①进行判断;把A点坐标代入y=-x2+2x+m+1中求出m,确定抛物线解析式,再通过解方程-x2+2x+3=0得到B点坐标,从而可对②进行判断;先确定抛物线的对称轴为直线x=1,则点P和点Q在对称轴两侧,所以点P到直线x=1的距离为1-x1,点Q到直线x=1的距离为x2-1,然后比较点Q点对称轴的距离和点P点对称轴的距离的大小,再根据二次函数的性质可对③进行判断.
解答 解:当a<x<b时,y>0,所以①错误;
当a=-1时,A点坐标为(-1,0),把A(-1,0)代入y=-x2+2x+m+1得-1-2+m+1=0,解得m=2,则抛物线解析式为y=-x2+2x+3,解方程-x2+2x+3=0得x1=-1,x2=3,则B(3,0),即b=3,所以②错误;
抛物线的对称轴为直线x=-$\frac{2}{2×(-1)}$=1,因为x1<1<x2,所以点P和点Q在对称轴两侧,点P到直线x=1的距离为1-x1,点Q到直线x=1的距离为x2-1,则x2-1-(1-x1)=x2+x1-2,而x1+x2>2,所以x2-1-(1-x1)>0,所以点Q到对称轴的距离比点P到对称轴的距离要大,所以y1>y2,所以③正确.
故选C.
点评 本题考查了抛物线与x轴的交点问题:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.判断点P、点Q到对称轴的距离的大小是判断命题③的真假的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
4.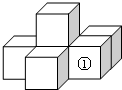 如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体从三个方向看的形状图,说法正确的是( )
如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体从三个方向看的形状图,说法正确的是( )
 如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体从三个方向看的形状图,说法正确的是( )
如图是由6个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体从三个方向看的形状图,说法正确的是( )| A. | 从正面看改变,从左面看改变 | B. | 从上面看不变,从左面看不变 | ||
| C. | 从正面看不变,从上面看不变 | D. | 从上面看改变,从左面看不变 |
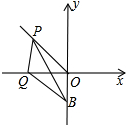 如图,已知B(0,-4)射线BO绕B点逆时针旋转30°,交第二象限角平分线于P点,线段PB绕P点顺时针旋转45°交x轴于Q点,求BQ长.
如图,已知B(0,-4)射线BO绕B点逆时针旋转30°,交第二象限角平分线于P点,线段PB绕P点顺时针旋转45°交x轴于Q点,求BQ长.
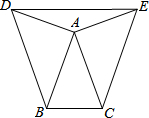 如图,已知AD=AE,∠BDE=∠CED,∠ABD=∠ACE.
如图,已知AD=AE,∠BDE=∠CED,∠ABD=∠ACE. 把棱长为1cm的若干个小正方体摆成如图所示的立方体图形.
把棱长为1cm的若干个小正方体摆成如图所示的立方体图形.