Question

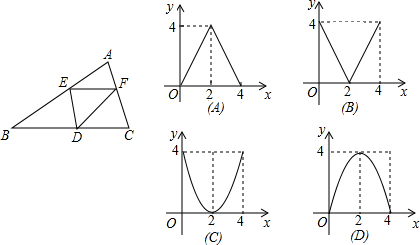
9．如图，在△ABC中，BC=8，BC上的高h=4，点D在BC上，EF∥BC，分别交AB、AC于点E、F（EF不过点A，B），设点E到BC的距离为x，△DEF的面积为y．
（1）y关于x的函数图象大致是（　　）；
（2）请你说明第（1）小题中你选择的理由．

Answer 1

分析 判断出△AEF和△ABC相似，根据相似三角形对应边成比例列式求出EF，再根据三角形的面积列式表示出S与x的关系式，然后得到大致图象选择即可．

解答 解：（1）y关于x的函数图象大致是（D）；
（2）理由：∵EF∥BC，
∴△AEF∽△ABC，
∴$\frac{EF}{BC}$=$\frac{4-x}{4}$，
∴EF=$\frac{4-x}{4}$•8=8-2x，
∴S=$\frac{1}{2}$（8-2x）•x=-x²+4x=-（x-2）²+4，
∴S与x的关系式为S=-（x-2）²+4（0＜x＜4），
纵观各选项，只有（D）选项图象符合．

点评 本题考查了动点问题函数图象，主要利用了相似三角形的性质，求出S与x的函数关系式是解题的关键，也是本题的难点．