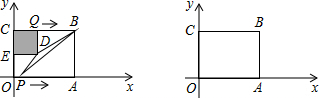题目内容
5.已知点P(a-2,b+3),Q(2a+1,3b-1),(P与Q不重合)(1)若PQ∥y轴,则a≠-3,b=2;
(2)若PQ⊥y轴,则a=-3,b≠2;
(3)若P,Q在第一、三象限夹角平分线上,则a=17,b=12.
分析 (1)由PQ∥y轴知P,Q的横坐标不同、纵坐标相等,即a-2≠2a+1,b+3=3b-1,解之可得;
(2)由PQ⊥y轴知P,Q的横坐标相等、纵坐标不同,即a-2=2a+1,b+3≠3b-1,解之可得;
(3)由P,Q在第一、三象限夹角平分线上知点P、Q两点的横纵坐标分别相等,从而列出方程组,解方程组即可得.
解答 解:(1)若PQ∥y轴,则P,Q的横坐标不同,纵坐标相等,
即a-2≠2a+1,b+3=3b-1,
解得:a≠-3,b=2,
故答案为:≠-3,=2;
(2)若PQ⊥y轴,则P,Q的横坐标相等,纵坐标不同,
即a-2=2a+1,b+3≠3b-1,
解得:a=-3,b≠2,
故答案为:=-3,≠2;
(3)若P,Q在第一、三象限夹角平分线上,则点P、Q两点的横纵坐标分别相等,
即$\left\{\begin{array}{l}{a-2=b+3}\\{2a+1=3b-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=17}\\{b=12}\end{array}\right.$,
故答案为:=17,=12.
点评 本题主要考查坐标与图形的性质,熟练掌握平行于坐标轴上的点及位于直线y=±x上的点的坐标特征是解题的关键

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
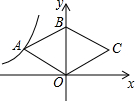 如图,菱形OABC的顶点O是原点,点B在y轴正半轴上,函数y=-$\frac{6}{x}$(x<0)的图象经过点A,则菱形OABC的面积为12.
如图,菱形OABC的顶点O是原点,点B在y轴正半轴上,函数y=-$\frac{6}{x}$(x<0)的图象经过点A,则菱形OABC的面积为12. 如图是一个立体图形的从正、左、上面看到的平面图形,请写出这个立体图形的名称,并计算这个立体图形的体积(结果保留π).
如图是一个立体图形的从正、左、上面看到的平面图形,请写出这个立体图形的名称,并计算这个立体图形的体积(结果保留π).
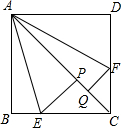 如图,在正方形ABCD内,以A为顶点作∠EAF=45°.设这个角的两边分别交正方形的边BC、CD于E、F,自E、F分别作正方形AC的垂线,垂足为P、Q.求证:过B、P、Q所作的圆的圆心在BC上.
如图,在正方形ABCD内,以A为顶点作∠EAF=45°.设这个角的两边分别交正方形的边BC、CD于E、F,自E、F分别作正方形AC的垂线,垂足为P、Q.求证:过B、P、Q所作的圆的圆心在BC上.