题目内容
17. 在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).
在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).(1)画出△ABC.
(2)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1,并求出△ABC在上述旋转过程中扫过的面积.
分析 (1)直接利用已知点在坐标系中找出连接即可;
(2)直接利用旋转的性质得出对应点位置进而得出答案,再利用扇形面积以及三角形面积求法得出答案.
解答 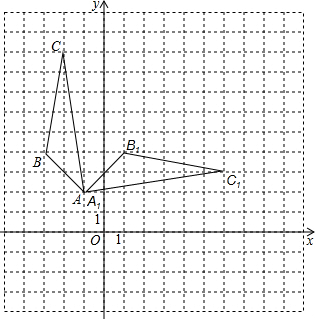 解:(1)如图所示:△ABC,即为所求;
解:(1)如图所示:△ABC,即为所求;
(2)如图所示:△A1B1C1,即为所求,
△ABC在上述旋转过程中扫过的面积为:
S△ABC+S扇形CAC1
=2×7-$\frac{1}{2}$×2×2-$\frac{1}{2}$×1×5-$\frac{1}{2}$×1×7+$\frac{90π×(5\sqrt{2})^{2}}{360}$
=6+$\frac{25π}{2}$.
点评 此题主要考查了旋转的性质以及三角形、扇形面积求法,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
7.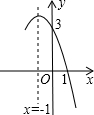 抛物线y=-x2+bx+c的部分图象如图所示,对称轴为x=-1,若y>0,则x的取值范围是( )
抛物线y=-x2+bx+c的部分图象如图所示,对称轴为x=-1,若y>0,则x的取值范围是( )
 抛物线y=-x2+bx+c的部分图象如图所示,对称轴为x=-1,若y>0,则x的取值范围是( )
抛物线y=-x2+bx+c的部分图象如图所示,对称轴为x=-1,若y>0,则x的取值范围是( )| A. | -3<x<1 | B. | x<-3或x>1 | C. | -4<x<l | D. | x<-4或x>1 |
5. 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )| A. | $\sqrt{6}$ | B. | 2$\sqrt{6}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
12.平面直角坐标系内一点P(-2,3)关于原点对称的点的坐标是( )
| A. | (3,-2) | B. | (2,-3) | C. | (-2,-3) | D. | (2,3) |
6.若|a|=3,|b|=4,且a<b,则a+b的值为( )
| A. | 7 | B. | ±7 | C. | ±1或±7 | D. | 1或7 |
7. 如图,菱形ABD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )
如图,菱形ABD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )
 如图,菱形ABD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )
如图,菱形ABD的周长为8cm,高AE长为$\sqrt{3}$cm,则对角线AC长和BD长之比为( )| A. | 1:$\sqrt{3}$ | B. | 1:$\sqrt{2}$ | C. | 1:3 | D. | 1:2 |
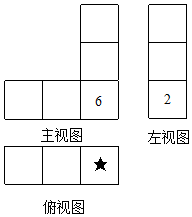 一个不透明立方体的6个面上分别写有数字1、2、3、4、5、6,任意两对面上所写的两个数字之和为7,将这样的几个立方体按照相接触两个面上的数字之和为8,摆放成一个几何体,这个几何体的三视图如图所示,图中所标注的是部分面上所见的数字,则★所代表的数是( )
一个不透明立方体的6个面上分别写有数字1、2、3、4、5、6,任意两对面上所写的两个数字之和为7,将这样的几个立方体按照相接触两个面上的数字之和为8,摆放成一个几何体,这个几何体的三视图如图所示,图中所标注的是部分面上所见的数字,则★所代表的数是( )
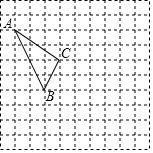 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,6),(-1,4).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,6),(-1,4).