题目内容
6.已知平面直角坐标系中,O是坐标原点,一次函数y=kx+b的图象与反比例函数y=$\frac{4}{x}$的图象交于点A(m,2),B(-1,n).(1)求m,n的值;
(2)求一次函数的表达式;
(3)求△OAB的面积.
分析 (1)把A(m,2),B(-1,n)代入反比例函数y=$\frac{4}{x}$,即可得到结果;
(2)由一次函数y=kx+b的图象过A(2,2),B(-1,-4),把A,B两点的坐标代入即可得到结论;
(3)根据三角形的面积公式即可求得.
解答 解:(1)∵A(m,2),B(-1,n)在反比例函数y=$\frac{4}{x}$的图象上,
∴2=$\frac{4}{m}$,n=$\frac{4}{-1}$,
∴m=2,n=-4;
(2)∵一次函数y=kx+b的图象过A(2,2),B(-1,-4),
∴$\left\{\begin{array}{l}{2=2k+b}\\{-4=-k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=2}\\{b=-2}\end{array}\right.$,
∴一次函数的表达式为:y=2x-2;
(3)S△AOB=$\frac{1}{2}$×2×2+$\frac{1}{2}×2×1$=3.
点评 本题考查了反比例函数与一次函数的交点问题,根据函数的解析式求点的坐标,待定系数法求函数的解析式,三角形面积的求法,熟练掌握待定系数法求函数解析式是解题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
14.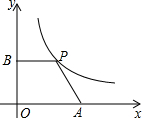 如图,在平面直角坐标系中,点A是x轴正半轴上的一定点,点P是反比例函数y=$\frac{4}{x}$(x>0)图象上的一个动点,PB⊥y轴于点B,当点P的横坐标的值逐渐减小时,四边形OAPB的面积将会( )
如图,在平面直角坐标系中,点A是x轴正半轴上的一定点,点P是反比例函数y=$\frac{4}{x}$(x>0)图象上的一个动点,PB⊥y轴于点B,当点P的横坐标的值逐渐减小时,四边形OAPB的面积将会( )
 如图,在平面直角坐标系中,点A是x轴正半轴上的一定点,点P是反比例函数y=$\frac{4}{x}$(x>0)图象上的一个动点,PB⊥y轴于点B,当点P的横坐标的值逐渐减小时,四边形OAPB的面积将会( )
如图,在平面直角坐标系中,点A是x轴正半轴上的一定点,点P是反比例函数y=$\frac{4}{x}$(x>0)图象上的一个动点,PB⊥y轴于点B,当点P的横坐标的值逐渐减小时,四边形OAPB的面积将会( )| A. | 逐渐减小 | B. | 逐渐增大 | C. | 不变 | D. | 先减小后增大 |
1.已知数据x1,x2,…,xn的平均数是2,方差是3,则一组新数据x1+8,x2+8,…,xn+8的平均数和方差分别是( )
| A. | 10,3 | B. | 10,11 | C. | 2,3 | D. | 2,11 |
11.计算(-x3)2所得结果是( )
| A. | x5 | B. | -x5 | C. | x6 | D. | -x6 |
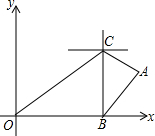 中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).
中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).