题目内容
14．
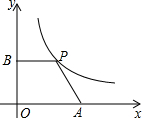如图，在平面直角坐标系中，点A是x轴正半轴上的一定点，点P是反比例函数y=$\frac{4}{x}$（x＞0）图象上的一个动点，PB⊥y轴于点B，当点P的横坐标的值逐渐减小时，四边形OAPB的面积将会（ ）| A． | 逐渐减小 | B． | 逐渐增大 | C． | 不变 | D． | 先减小后增大 |
分析 由双曲线y=$\frac{4}{x}$（x＞0）设出点P的坐标，运用坐标表示出四边形OAPB的面积函数关系式即可判定．
解答 解：设点P的坐标为（x，$\frac{4}{x}$），
∵PB⊥y轴于点B，点A是x轴正半轴上的一个定点，
∴四边形OAPB是个直角梯形，
∴四边形OAPB的面积=$\frac{1}{2}$（PB+AO）•BO=$\frac{1}{2}$（x+AO）•$\frac{4}{x}$=2+$\frac{2AO}{x}$=2+2AO•$\frac{1}{x}$，
∵AO是定值，
∴四边形OAPB的面积是个增函数，即点P的横坐标逐渐减小时四边形OAPB的面积逐渐增大．
故选：B．
点评 本题主要考查了反比例函数系数k的几何意义，解题的关键是运用点的坐标求出四边形OAPB的面积的函数关系式．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
5．下列式子为最简二次根式的是（ ）
| A． | $\sqrt{\frac{x}{2}}$ | B． | $\sqrt{27}$ | C． | $\sqrt{{x}^{2}-4}$ | D． | $\sqrt{{2x}^{2}y}$ |
2．若关于x的分式方程$\frac{x-6}{x-5}+1=\frac{k}{5-x}$有增根，则k的值是（ ）
| A． | -1 | B． | -2 | C． | 2 | D． | 1 |
9．代数式$\frac{\sqrt{x-1}}{2}$在实数范围内有意义，则x的取值范围为（ ）
| A． | x≥1 | B． | x≥-1 | C． | x≥$\frac{1}{2}$ | D． | x≥-$\frac{1}{2}$ |
19．将$\sqrt{{3}^{2}×8}$化简，正确的结果是（ ）
| A． | 3$\sqrt{8}$ | B． | ±3$\sqrt{8}$ | C． | 6$\sqrt{2}$ | D． | ±3$\sqrt{2}$ |
