题目内容
Rt△ABC中,∠C=90°,AC=6,BC=8,则AB上的高为 ,AB,AC上的中线分别为 .
考点:勾股定理
专题:
分析:作出图形,利用勾股定理列式求出AB,再根据△ABC的面积列出方程求解即可;
根据直角三角形斜边上的中线等于斜边的一半可得AB边上的中线等于AB的一半,利用勾股定理列式计算即可求出AC边上的中线长.
根据直角三角形斜边上的中线等于斜边的一半可得AB边上的中线等于AB的一半,利用勾股定理列式计算即可求出AC边上的中线长.
解答: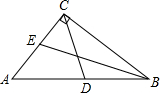 解:如图,∵∠C=90°,AC=6,BC=8,
解:如图,∵∠C=90°,AC=6,BC=8,
∴AB=
=
=10,
设AB上的高为h,
则S△ABC=
AB•h=
AC•BC,
即
×10•h=
×6×8,
解得h=4.8,
所以,AB上的高为4.8,
AB边上的中线CD=
AB=
×10=5,
∵BE是AC边上的中线,
∴CE=
AC=
×6=3,
在Rt△BCE中,由勾股定理得,BE=
=
=
.
故答案为:4.8,5和
.
 解:如图,∵∠C=90°,AC=6,BC=8,
解:如图,∵∠C=90°,AC=6,BC=8,∴AB=
| AC2+BC2 |
| 62+82 |
设AB上的高为h,
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
解得h=4.8,
所以,AB上的高为4.8,
AB边上的中线CD=
| 1 |
| 2 |
| 1 |
| 2 |
∵BE是AC边上的中线,
∴CE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△BCE中,由勾股定理得,BE=
| BC2+CE2 |
| 82+32 |
| 73 |
故答案为:4.8,5和
| 73 |
点评:本题考查了勾股定理,直角三角形斜边上的中线等于斜边的一半的性质,熟记定理与性质是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
 有理数a、b在数轴上的位置如图,化简:|a|+|b|-|a+b|=
有理数a、b在数轴上的位置如图,化简:|a|+|b|-|a+b|= 如图所示,A、B、C、D是⊙O上顺次四点,若∠AOC=160°,则∠D=
如图所示,A、B、C、D是⊙O上顺次四点,若∠AOC=160°,则∠D= 菱形ABCD的对角线交于点O,同时菱形中的两条线段也交于点O,探索当∠EOF具有怎样的特征时,EM=NF,并说明理由.
菱形ABCD的对角线交于点O,同时菱形中的两条线段也交于点O,探索当∠EOF具有怎样的特征时,EM=NF,并说明理由.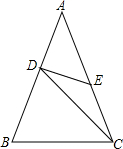 如图,在△ABC中,AB=AC,AD=ED=EC,CD=BC,求△ABC各角的度数.(提示:设∠DCE=x)
如图,在△ABC中,AB=AC,AD=ED=EC,CD=BC,求△ABC各角的度数.(提示:设∠DCE=x)