题目内容
9.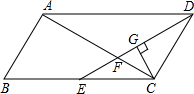 如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}\sqrt{3}$cm,则EF的长为( )
如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}\sqrt{3}$cm,则EF的长为( )| A. | 2cm | B. | $\sqrt{3}$cm | C. | 1cm | D. | $\frac{2}{3}\sqrt{3}$cm |
分析 利用平行四边形的性质以及角平分线的性质得出∠CDE=∠CED,进而求出DE的长,再利用相似三角形的判定与性质得出EF的长.
解答 解:∵在?ABCD中,∠ADC的平分线DE交BC于点E,
∴∠ADE=∠EDC,∠ADE=∠DEC,AB=DC,
∴∠CDE=∠CED,
∵AB=3cm,AD=6cm,
∴DC=EC=3cm,
∵CG⊥DE,DG=$\frac{3\sqrt{3}}{2}$cm,
∴EG=$\frac{3\sqrt{3}}{2}$cm,
∴DE=3$\sqrt{3}$cm,
∵AD∥BC,
∴△AFD∽△CFE,
∴$\frac{AD}{EC}=\frac{DF}{EF}$,则$\frac{6}{3}=\frac{3\sqrt{3}-EF}{EF}$,
解得:EF=$\sqrt{3}$.
故选:B.
点评 此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识,得出△AFD∽△CFE是解题关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
18.下列说法正确的是( )
| A. | 两点之间的距离是两点间的线段 | |
| B. | 同一平面内,过一点有且只有一条直线与已知直线平行 | |
| C. | 与同一条直线垂直的两条直线也垂直 | |
| D. | 同一平面内,过一点有且只有一条直线与已知直线垂直 |
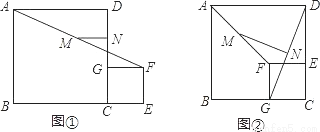


 如图,在平行四边形ABCD中,AB=5,BC=12,对角线交于点O,∠BAD的平分线交BC于E、交BD于F,分别过顶点B、D作AE的垂线,垂足为G、H,连接OG、OH.
如图,在平行四边形ABCD中,AB=5,BC=12,对角线交于点O,∠BAD的平分线交BC于E、交BD于F,分别过顶点B、D作AE的垂线,垂足为G、H,连接OG、OH.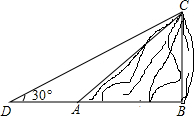 如图,某人在D处测得山顶C的仰角为30°,向前走30米到达山脚A处,测得山坡AC的坡度为i=1:1.5,求山顶的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).
如图,某人在D处测得山顶C的仰角为30°,向前走30米到达山脚A处,测得山坡AC的坡度为i=1:1.5,求山顶的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数). 已知双曲线y=$\frac{k}{x}$和直线y=ax+b相交于A(-1,4)和B(2,m)两点,试确定双曲线和直线的函数关系式.
已知双曲线y=$\frac{k}{x}$和直线y=ax+b相交于A(-1,4)和B(2,m)两点,试确定双曲线和直线的函数关系式.