题目内容
14.随着互联网的普及,某手机厂商采用先网络预定,然后根据订单量生产手机的方式销售,2015年该厂商将推出一款新手机,根据相关统计数据预测,定价为2200元,日预订量为20000台,若定价每减少100元,则日预订量增加10000台.(1)设定价减少x元,预订量为y台,写出y与x的函数关系式;
(2)若每台手机的成本是1200元,求所获的利润w(元)与x(元)的函数关系式,并说明当定价为多少时所获利润最大;
(3)若手机加工成每天最多加工50000台,且每批手机会有5%的故障率,通过计算说明每天最多接受的预订量为多少?按最大量接受预订时,每台售价多少元?
分析 (1)根据题意列代数式即可;
(2)根据利润=单台利润×预订量,列出函数表达式,根据二次函数性质解决定价为多少时所获利润最大;
(3)根据题意列式计算每天最多接受的预订量,根据每天最多接受的预订量列方程求出最大量接受预订时每台售价即可.
解答 解:(1)根据题意:y=20000+$\frac{x}{100}$×10000=100x+20000;
(2)设所获的利润w(元),则W=(20000-1200-x)(100x+20000)=-100(x-400)2+36000000;
所以当降价400元,即定价为2200-400=1800元时,所获利润最大;
(2)根据题意每天最多接受50000(1-0.05)=47500台,
此时47500=100x+20000,
解得:x=275.
所以最大量接受预订时,每台定价2200-275=1925元.
点评 本题主要考查了函数实际应用问题,涉及到列代数式、求函数关系式、二次函数的性质、一元一次方程应用等知识,弄清题意,找出数量关系是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.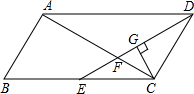 如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}\sqrt{3}$cm,则EF的长为( )
如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}\sqrt{3}$cm,则EF的长为( )
 如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}\sqrt{3}$cm,则EF的长为( )
如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}\sqrt{3}$cm,则EF的长为( )| A. | 2cm | B. | $\sqrt{3}$cm | C. | 1cm | D. | $\frac{2}{3}\sqrt{3}$cm |
19.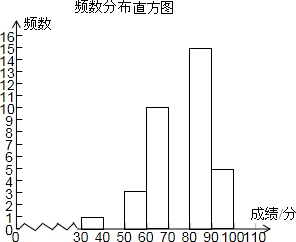 如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
频数分布表
(1)以上分组的组距=10
(2)请补全频数分布表和频数分布直方图;
(3)请计算这50名同学的平均成绩;
(4)请你估计该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数.
 如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
如图,某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.频数分布表
| 成绩分组 | 频数 | 频率 |
| 30≤x<40 | 1 | 0.02 |
| 40≤x<50 | 1 | 0.02 |
| 50≤x<60 | 3 | 0.06 |
| 60≤x<70 | 10 | 0.2 |
| 70≤x<80 | 15 | 0.3 |
| 80≤x<90 | 15 | 0.3 |
| 90≤x<100 | 5 | 0.1 |
| 合计 | 50 | 1 |
(2)请补全频数分布表和频数分布直方图;
(3)请计算这50名同学的平均成绩;
(4)请你估计该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数.
 .
.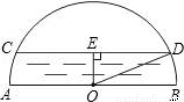
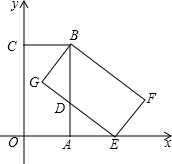 如图,已知在直角坐标系中,矩形OABC的边OA在x轴正半轴上,边OC在y轴的正半轴上,B点的坐标为(4,8),将矩形OABC绕点B逆时针旋转得到矩形EFBG,点E恰好落在x轴上.
如图,已知在直角坐标系中,矩形OABC的边OA在x轴正半轴上,边OC在y轴的正半轴上,B点的坐标为(4,8),将矩形OABC绕点B逆时针旋转得到矩形EFBG,点E恰好落在x轴上.


