Question

17．我们知道，一次函数y=x+1的图象可以由正比例函数y=x的图象向左平移1个单位得到；爱动脑的小聪认为：函数y=$\frac{2}{x+1}$也可以由反比例函数y=$\frac{2}{x}$通过平移得到，小明通过研究发现，事实确实如此，并指出了平移规律，即只要把y=$\frac{2}{x}$（双曲线）的图象向左平移1个单位（如图1虚线所示），同时函数y=$\frac{2}{x+1}$的图象上下都无限逼近直线x=-1．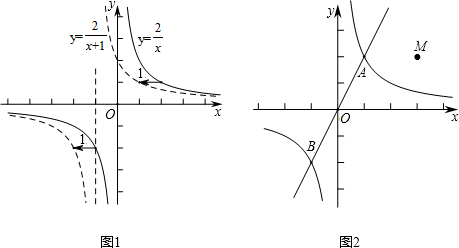

如图2，已知反比例函C：y=$\frac{{k}_{1}}{x}$与正比例函数L：y=k₂x的图象相交于点A（1，2）和点B．
（1）写出点B的坐标，并求k₁和k₂的值；
（2）将函数y=$\frac{{k}_{1}}{x}$的图象C与直线L同时向右平移n（n＞0）个单位长度，得到的图象分别记为C′和L′，已知图象L′经过点M（3，2）；
则①n的值为；②写出平移后的图象C′对应的函数关系式为y=$\frac{2}{x-2}$；
③利用图象，直接写出不等式$\frac{2}{x-2}$＞2x-4的解集为x＜1或2＜x＜3．

Answer 1

分析 （1）由反比例函数的对称性根据A的坐标求出B的坐标，把A坐标代入反比例解析式求出k₁的值，代入正比例解析式求出k₂的值即可；
（2）①利用平移规律表示出直线L′解析式，把M坐标代入求出n的值即可；②把n的值代入即可确定出C′解析式；③画出两函数图象，找出反比例函数图象位于一次函数图象上方时x的范围即可．

解答 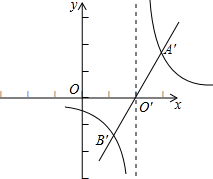解：（1）由对称性得到B（-1，-2），
把A（1，2）代入反比例解析式得：k₁=2，代入正比例解析式得：k₂=2；
（2）①直线L向右平移n个单位，得到y=2（x-n），
把M（3，2）代入得：2=2（3-n），即n=2；
②平移后的图象C′对应的函数关系式为y=$\frac{2}{x-2}$；
③如图所示，由平移规律得：A′（3，2），B′（1，-2），
则不等式$\frac{2}{x-2}$＞2x-4的解集为x＜1或2＜x＜3，
故答案为：（2）②y=$\frac{2}{x-2}$；③x＜1或2＜x＜3

点评 此题属于反比例函数综合题，涉及的知识有：反比例函数的性质，待定系数法确定函数解析式，以及平移规律，利用了数形结合的思想，熟练掌握平移规律是解本题的关键．