题目内容
11.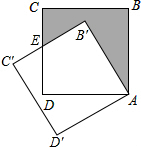 如图,将边长为$\sqrt{3}$的正方形ABCD绕点A逆时针方向旋转30°后得到正方形AB′C′D′.
如图,将边长为$\sqrt{3}$的正方形ABCD绕点A逆时针方向旋转30°后得到正方形AB′C′D′.(1)求证:ED=EB′;
(2)求图中阴影部分的面积.
分析 (1)根据HL即可证明△ADE≌△AB'E,根据全等三角形的对应边相等即可证得;
(2)求得∠EAD的度数,根据三角函数求得ED的长,则△ADE的面积即可求得,然后利用正方形的面积减去△ADE和△AB'E的面积即可求解.
解答 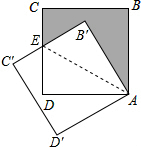 解:(1)连接AE.
解:(1)连接AE.
在直角△ADE和直角△AB'E中,
$\left\{\begin{array}{l}{AB'=AD}\\{AE=AE}\end{array}\right.$,
∴△ADE≌△AB'E,
∴DE=EB';
(2)∵△ADE≌△AB'E,
∴∠DAE=∠DAD',
又∵∠BAB'=30°,∠BAD=90°,
∴∠ADE=30°,
在直角△ADE中,ED=AD•tan30°=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=1,
则S△ADE=$\frac{1}{2}$AD•ED=$\frac{1}{2}$×$\sqrt{3}$×1=$\frac{\sqrt{3}}{2}$,
∴S△AB'E=S△ADE=$\frac{\sqrt{3}}{2}$,
又∵S正方形ABCD=($\sqrt{3}$)2=3,
∴S阴影=3-2×$\frac{\sqrt{3}}{2}$=3-$\sqrt{3}$.
点评 本题考查旋转的性质以及全等三角形的判定与性质,正确证明△ADE≌△AB'E是本题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
6.已知抛物线y=(x+2)2+h-4的顶点A在直线y=2x-1上,则抛物线的函数解析式是( )
| A. | y=x2-4x+7 | B. | y=x2+4x-1 | C. | y=x2-4x+9 | D. | y=x2+4x-3 |
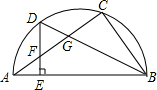 如图,AB是半圆的直径,AC是一条弦,D是$\widehat{AC}$的中点,DE⊥AB于E,交AC于F,DB交AC于G.求证:
如图,AB是半圆的直径,AC是一条弦,D是$\widehat{AC}$的中点,DE⊥AB于E,交AC于F,DB交AC于G.求证: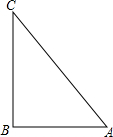 如图,在△ABC中,∠BAC=90°,AB=6,BC=12,点P从A点出发向B以1m/s的速度移动,点Q从B点出发向C点以2m/s的速度移动.如果P,Q分别从A,B两地同时出发,几秒后△PBQ与原三角形相似?
如图,在△ABC中,∠BAC=90°,AB=6,BC=12,点P从A点出发向B以1m/s的速度移动,点Q从B点出发向C点以2m/s的速度移动.如果P,Q分别从A,B两地同时出发,几秒后△PBQ与原三角形相似?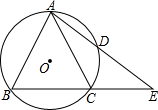 如图,⊙0是△ABC的外接圆,AB=AC,求证:AB2=AE•AD.
如图,⊙0是△ABC的外接圆,AB=AC,求证:AB2=AE•AD.