题目内容
6.已知抛物线y=(x+2)2+h-4的顶点A在直线y=2x-1上,则抛物线的函数解析式是( )| A. | y=x2-4x+7 | B. | y=x2+4x-1 | C. | y=x2-4x+9 | D. | y=x2+4x-3 |
分析 利用顶点式可得A的坐标为(-2,h-4),然后把A(-2,h-4)代入y=2x-1可求出h的值,从而可确定抛物线解析式.
解答 解:抛物线y=(x+2)2+h-4的顶点A的坐标为(-2,h-4),
把A(-2,h-4)代入y=2x-1得h-4=-4-1,解得h=-1,
所以抛物线的解析式为y=(x+2)2-5,即y=x2+4x-1.
故选B.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
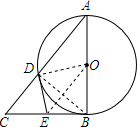 如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于D,DE切⊙O于D,交BC于E,求证:BE=CE.
如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于D,DE切⊙O于D,交BC于E,求证:BE=CE. 如图,A、B是⊙O上的两点,∠AOB=80°,C是⊙O上不与A、B重合的任一点,求∠ACB的度数.
如图,A、B是⊙O上的两点,∠AOB=80°,C是⊙O上不与A、B重合的任一点,求∠ACB的度数.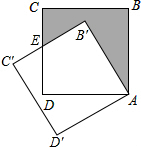 如图,将边长为$\sqrt{3}$的正方形ABCD绕点A逆时针方向旋转30°后得到正方形AB′C′D′.
如图,将边长为$\sqrt{3}$的正方形ABCD绕点A逆时针方向旋转30°后得到正方形AB′C′D′. 如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为x=2.
如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为x=2. 现有大小相同的正方形纸片30张,小亮用其中3张拼成一个如图所示的长方形,小芳也想拼一个与它形状相同但比它大的长方形,则她至少要用几张正方形纸片(不得把每个正方形纸片剪开)?你知道她可能拼出什么样的图形吗?请你试着画一画.
现有大小相同的正方形纸片30张,小亮用其中3张拼成一个如图所示的长方形,小芳也想拼一个与它形状相同但比它大的长方形,则她至少要用几张正方形纸片(不得把每个正方形纸片剪开)?你知道她可能拼出什么样的图形吗?请你试着画一画.