题目内容
5.探究:换元法是重要的数学思想方法,用换元法可解决许多数学问题,请看例题:解方程:x4-2x2-3=0.
解:设x2=y,则原方程化为y2-2y-3=0.
解关于y的一元二次方程,得y1=-1,y2=3.
当y=-1时,即x2=-1,此时方程无实数根;
当y=3时,即x2=3解得x1=$\sqrt{3}$,x2=-$\sqrt{3}$.
所以原方程的根是x1=$\sqrt{3}$,x2=-$\sqrt{3}$.
请你用换元法解下列方程:
(1)$\frac{1}{{x}^{2}}$-$\frac{5}{x}$+6=0;
(2)(x2-2)-2(x2-2)-8=0.
分析 (1)根据题意设$\frac{1}{x}=a$,即可解答此方程;
(2)根据题意设x2-2=8,即可解答此方程.
解答 解:(1)$\frac{1}{{x}^{2}}$-$\frac{5}{x}$+6=0
设$\frac{1}{x}=a$,
则a2-5a+6=0
解得,a1=2,a2=3,
∴$\frac{1}{x}=2$或$\frac{1}{x}=3$,
解得,${x}_{1}=\frac{1}{2},{x}_{2}=\frac{1}{3}$,
经检验${x}_{1}=\frac{1}{2},{x}_{2}=\frac{1}{3}$是原分式方程的解;
(2)(x2-2)-2(x2-2)-8=0,
设x2-2=a,
则a-2a-8=0,
解得,a=-8,
∴x2-2=8,
解得,${x}_{1}=\sqrt{10},{x}_{2}=-\sqrt{10}$.
点评 本题考查换元法解一元二次方程,解题的关键是明确换元法解一元二次方程的方法.

练习册系列答案
相关题目
16.一个三角形三个内角的度数比为1:2:1,这个三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰直角三角形 |
13.若关于x的方程2x+a-4=0的解是-2,则a的值等于( )
| A. | -8 | B. | 8 | C. | 0 | D. | 2 |
5.现定义一种运算“⊙”,对任意有理数m、n,规定:m⊙n=mn(m-n),如1⊙2=1×2(1-2)=-2,则(a+b)⊙(a-b)的值是( )
| A. | 2ab2-2b2 | B. | 2a2b-2b3 | C. | 2ab2+2b2 | D. | 2ab-2ab2 |
12.若对于任何实数a,b,c,d,定义$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,按照定义,若$|\begin{array}{l}{x+1}&{x}\\{x-1}&{2x-3}\end{array}|$=0,则x的值为( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 3 | D. | ±$\sqrt{3}$ |

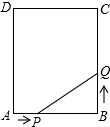 如图,矩形ABCD中,AB=6cm,BC=12cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动.如果P、Q分别是从A、B同时出发,
如图,矩形ABCD中,AB=6cm,BC=12cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动.如果P、Q分别是从A、B同时出发, 二次函数y=(x+m)2+n的图象如图,则反比例函数y=$\frac{mn}{x}$的图象经过第一、三象限.
二次函数y=(x+m)2+n的图象如图,则反比例函数y=$\frac{mn}{x}$的图象经过第一、三象限.