题目内容
如果m=(2+
)64,它的小数部分为p,则m(1-p)= .
| 3 |
考点:估算无理数的大小
专题:
分析:首先设n=(2-
)64,则m+n为正整数,进而得出m的整数部分为m+n-1,进而求出1-p=n,即可得出答案.
| 3 |
解答:解:∵m=(2+
)64,
设n=(2-
)64,则m+n为正整数,
又∵0<2-
<1,
∴0<n<1,
∴m<m+n<m+1,
∴m+n-1<m<m+n
∴m的整数部分为m+n-1,
∴p=m-(m+n-1)=-n+1
∴1-p=n
∴m(1-p)=mn=(
+2)64×(2-
)64=1.
故答案为:1.
| 3 |
设n=(2-
| 3 |
又∵0<2-
| 3 |
∴0<n<1,
∴m<m+n<m+1,
∴m+n-1<m<m+n
∴m的整数部分为m+n-1,
∴p=m-(m+n-1)=-n+1
∴1-p=n
∴m(1-p)=mn=(
| 3 |
| 3 |
故答案为:1.
点评:此题主要考查了估计无理数以及积的乘方等知识,得出m(1-p)=mn是解题关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由.
如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠1,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由.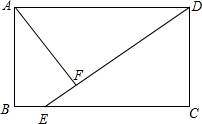 如图,在矩形ABCD中,点E在BC上,AF⊥DE于点F,且AF=3,CD=5,DE=15.求矩形ABCD的面积.
如图,在矩形ABCD中,点E在BC上,AF⊥DE于点F,且AF=3,CD=5,DE=15.求矩形ABCD的面积.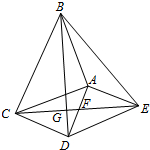 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中: 如图,矩形OABC是一把粉刷墙壁用的刷子,其中OA=3,OC=4,若一工人在一次粉刷时仅把矩形刷子靠在墙上绕点O旋转90°,则墙壁该次被粉刷的面积是
如图,矩形OABC是一把粉刷墙壁用的刷子,其中OA=3,OC=4,若一工人在一次粉刷时仅把矩形刷子靠在墙上绕点O旋转90°,则墙壁该次被粉刷的面积是 如图,AB=BC=CA=AD,则∠BDC=
如图,AB=BC=CA=AD,则∠BDC=